Introduction.
In previous post, I reproduced the Laminar Flow of the transition state in PINNs using the governing equations of the VP form with reference to the paper, but the results were very different from the values in the reference paper. This time, I also performed it with the governing equations of ST form, and I will summarize the results in this post.
Sources
- PINN-laminar-flow/PINN_unsteady - a paper that I have been referring to as a source of information and github. the Cauchy stress tensor part of this paper (continuum-mechanics-based formulation), i.e. equations (3) and (4), tripped me up.
- On Physics-Informed Deep Learning for Solving Navier-Stokes Equations - The paper referenced from this page describes two types of Navier-Stokes equations (VP form and ST form). However, the problem setup in this paper deals with the steady state and does not include the time variable $t$.
Physical Background
Please refer to this posting for more information on VP and ST types (with links to reference papers).
Cauchy stress tensor (ST) form
I tried to represent equations (3) and (4) in Source 1 in 2D component notation in order to code them as governing equations. However, I could not do so, so I read the Github code of Source 1 and obtained the following governing equations. Equations (3) and (4) in Source 1. that I had stumbled upon are as follows.
$$ \frac{\partial \boldsymbol{v}}{\partial t} + (\boldsymbol{v}\cdot\nabla)\boldsymbol{v} = \frac{1}{\rho}\nabla\cdot\boldsymbol{\sigma} + \boldsymbol{g} \tag{1} $$
$$ \boldsymbol{\sigma} = -p\boldsymbol{I} + \mu(\nabla\boldsymbol{v}+\nabla\boldsymbol{v}^{T}) \tag{2} $$
Let ‘p_NN()’ be the function for the neural net used in PINNs this time, ‘p_NN()’ is a function that maps space-time variables to mixed variables. It is expressed as follows. $$ (x, y, t) \longmapsto (\psi, p, \sigma_{11}, \sigma_{22}, \sigma_{12}) \tag{3} $$ where $\psi$ is the stream function and the velocities are $u = \frac{\partial \psi}{\partial y}$ and $v = - \frac{\partial \psi}{\partial x}$. This says that the continuity equation is automatically satisfied (from the paper in Source 1.). The $p$ is the pressure. The governing equations are shown below using $\sigma_{11},\sigma_{22},\sigma_{12}$. In the following notation, for example, $\partial_t u$ denotes $\frac{\partial u}{\partial t}$.
$$ f_u = \rho \partial_t u + \rho(u\partial_x u + v\partial_y u) - \partial_x \sigma_{11} - \partial_y \sigma_{12} \tag{4} $$
$$ f_v = \rho \partial_t v + \rho(u\partial_x v + v\partial_y v) - \partial_x \sigma_{12} - \partial_y \sigma_{22} \tag{5} $$
$$ f_{xx} = -p + 2\mu\partial_x u - \sigma_{11} \tag{6} $$
$$ f_{yy} = -p + 2\mu\partial_y v - \sigma_{22} \tag{7} $$
$$ f_{xy} = \mu(\partial_y u + \partial_x v) - \sigma_{12} \tag{8} $$
$$ f_p = p + \frac{1}{2}(\sigma_{11}+\sigma_{22}) \tag{9} $$
If equation (3) is used as a loss function and learning proceeds in the direction of minimizing them, we end up with a function ‘p_NN()’expressed on a neural net that represents the environment (domain, boundary conditions) in question.
Code
Only the parts that differ from the previous this post are listed.
Create network classes for all coupling layers
# define p_NN class
class p_NN(nn.Module):
def __init__(self, n_input, n_output, n_hiddens=[32,64,128,128,64,32]):
super().__init__()
self.activation = nn.Tanh()
self.input_layer = nn.Linear(n_input, n_hiddens[0])
self.hidden_layers = nn.ModuleList(
[nn.Linear(n_hiddens[i], n_hiddens[i+1]) for i in range(len(n_hiddens)-1)]
)
self.output_layer = nn.Linear(n_hiddens[-1], n_output)
def forward(self, x):
x = self.activation(self.input_layer(x))
for layer in self.hidden_layers:
x = self.activation(layer(x))
x = self.output_layer(x)
return x
def neural_net(self, x, y, t):
inputs = torch.cat([x, y, t], dim=1)
outputs = self.forward(inputs)
psi = outputs[:, 0:1]
p = outputs[:, 1:2]
s11 = outputs[:, 2:3]
s22 = outputs[:, 3:4]
s12 = outputs[:, 4:5]
return psi, p, s11, s22, s12
def net_uvp(self, x, y, t):
x.requires_grad = True
y.requires_grad = True
t.requires_grad = True
psi, p, s11, s22, s12 = self.neural_net(x, y, t)
u = gradients(psi, y)
v = -gradients(psi, x)
return u, v, p, s11, s22, s12
def net_f(self, x, y, t):
u, v, p, s11, s22, s12 = self.net_uvp(x, y, t)
u_x = gradients(u, x)
u_y = gradients(u, y)
u_t = gradients(u, t)
s11_x = gradients(s11, x)
s12_y = gradients(s12, y)
fu = rho*u_t + rho*(u*u_x + v*u_y) - (s11_x + s12_y)
v_x = gradients(v, x)
v_y = gradients(v, y)
v_t = gradients(v, t)
s12_x = gradients(s12, x)
s22_y = gradients(s22, y)
fv = rho*v_t + rho*(u*v_x + v*v_y) - (s12_x + s22_y)
fxx = -p + mu*2.0*u_x - s11
fyy = -p + mu*2.0*v_y - s22
fxy = mu*(u_y + v_x) - s12
fp = p + (s11 + s22)/2.0
return fu, fv, fxx, fyy, fxy, fp
def predict(self, x, y, t): # no tensor is passed, return no tensor
xx = torch.tensor(x, device=device, dtype=torch.float32)
yy = torch.tensor(y, device=device, dtype=torch.float32)
tt = torch.tensor(t, device=device, dtype=torch.float32)
uu, vv, pp, _, _, _ = self.net_uvp(xx, yy, tt)
u = uu.to("cpu").detach().numpy()
v = vv.to("cpu").detach().numpy()
p = pp.to("cpu").detach().numpy()
return u, v, p
Only neural_net(), net_uvp(), and net_f() were modified to apply the governing equations described in “Physical Background”. The argument taking part of the sections calling these functions has also been changed.
Define loss function and optimizer function
# Loss function: Mean Square Error
loss_func = nn.MSELoss()
# Optimizer: Adam(Adaptive moment estimation)
optimizer = optim.Adam(model.parameters(), lr=0.0005)
# scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=0.98)
In this study, the learning rate was set to 0.0005 in conjunction with Source 1.
Learning loop
# learning Loop
num_epoch = 30000 # epoch count
Epoch = []
Loss_fv = []
Loss_fu = []
Loss_fxx = []
Loss_fyy = []
Loss_fxy = []
Loss_fp = []
Loss_PINN = []
Loss_TOTAL = []
Loss_IC = []
Loss_WALL = []
Loss_INLET = []
Loss_OUTLET = []
for i in range(num_epoch):
if i == 0:
print("Epoch \t Loss_Total \t Loss_PINN \t Loss_IC \t Loss_WALL \t Loss_INLET \t Loss_OUTLET")
optimizer.zero_grad()
fu, fv, fxx, fyy, fxy, fp = model.net_f(x_c, y_c, t_c)
loss_fu = torch.mean(fu**2)
loss_fv = torch.mean(fv**2)
loss_fxx = torch.mean(fxx**2)
loss_fyy = torch.mean(fyy**2)
loss_fxy = torch.mean(fxy**2)
loss_fp = torch.mean(fp**2)
loss_PINN = loss_fu + loss_fv + loss_fxx + loss_fyy + loss_fxy + loss_fp
u_ic, v_ic, p_ic, _, _, _ = model.net_uvp(x_IC, y_IC, t_IC)
loss_IC = torch.mean(u_ic**2) + torch.mean(v_ic**2) + torch.mean(p_ic**2)
u_wall, v_wall, _, _, _, _ = model.net_uvp(x_WALL, y_WALL, t_WALL)
loss_WALL = torch.mean(u_wall**2) + torch.mean(v_wall**2)
u_inlet, v_inlet, _, _, _, _ = model.net_uvp(x_INLET, y_INLET, t_INLET)
loss_INLET = torch.mean((u_inlet - u_INLET)**2) + torch.mean(v_inlet**2)
_, _, p_outlet, _, _, _ = model.net_uvp(x_OUTLET, y_OUTLET, t_OUTLET)
loss_OUTLET = torch.mean(p_outlet**2)
loss_TOTAL = loss_PINN + loss_IC + 5*loss_WALL + 5*loss_INLET + loss_OUTLET
loss_TOTAL.backward()
optimizer.step()
if i % 100 == 0:
Epoch.append(i)
Loss_fu.append(loss_fu.detach().cpu().numpy())
Loss_fv.append(loss_fv.detach().cpu().numpy())
Loss_fxx.append(loss_fxx.detach().cpu().numpy())
Loss_fyy.append(loss_fyy.detach().cpu().numpy())
Loss_fxy.append(loss_fxy.detach().cpu().numpy())
Loss_fp.append(loss_fp.detach().cpu().numpy())
Loss_PINN.append(loss_PINN.detach().cpu().numpy())
Loss_TOTAL.append(loss_TOTAL.detach().cpu().numpy())
Loss_IC.append(loss_IC.detach().cpu().numpy())
Loss_WALL.append(loss_WALL.detach().cpu().numpy())
Loss_INLET.append(loss_INLET.detach().cpu().numpy())
Loss_OUTLET.append(loss_OUTLET.detach().cpu().numpy())
if i % 1000 == 0:
print(i, "\t",
format(loss_TOTAL.detach().cpu().numpy(), ".4E"), "\t",
format(loss_PINN.detach().cpu().numpy(), ".4E"), "\t",
format(loss_IC.detach().cpu().numpy(), ".4E"), "\t",
format(loss_WALL.detach().cpu().numpy(), ".4E"), "\t",
format(loss_INLET.detach().cpu().numpy(), ".4E"), "\t",
format(loss_OUTLET.detach().cpu().numpy(), ".4E"), "\t",
)
In the learning loop section above, the part that receives the return values of net_f(), the part that calculates the loss of the governing equations from them, and the part that calls neural_net() were changed to net_uvp(). These changes were made in response to the governing equation changes.
In conjunction with source 1, WALL and INLET were weighted in the part where total loss is calculated.
The training loop was increased to 50,000 times in order to obtain results with sufficiently advanced learning.
Visualization results
Results with ST type
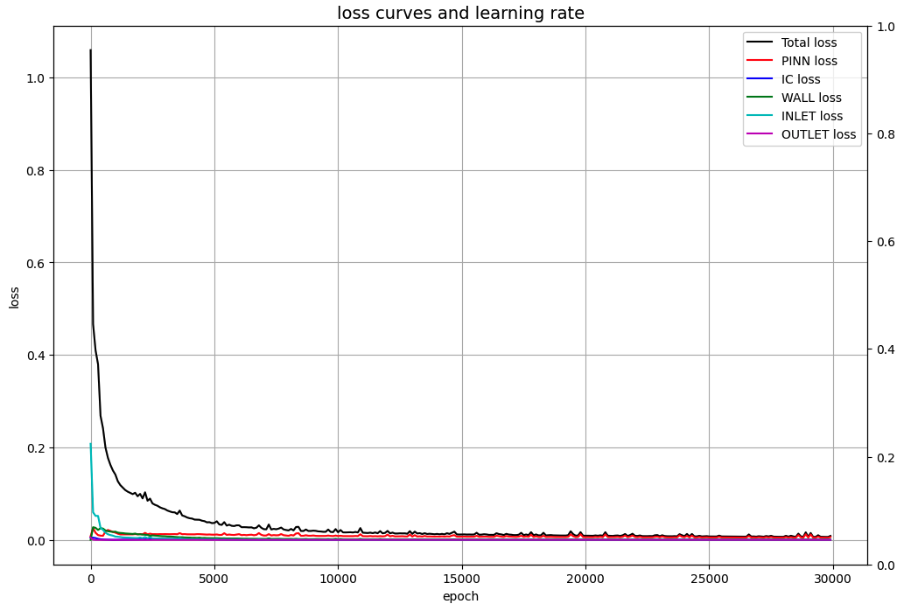
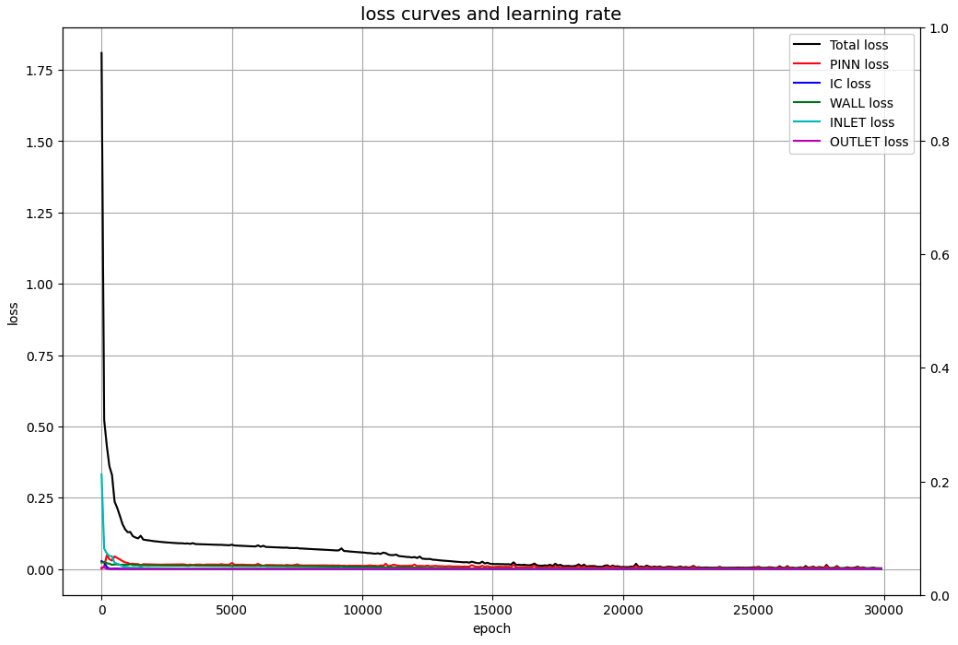
Loss curves
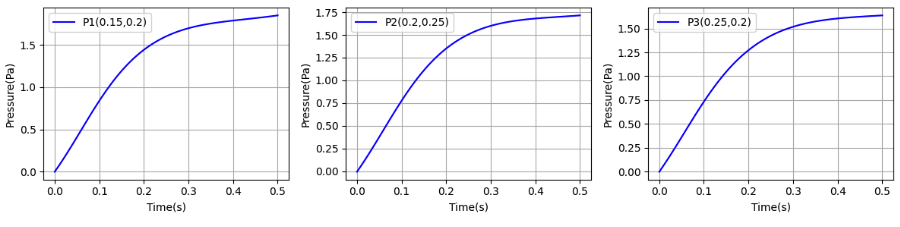
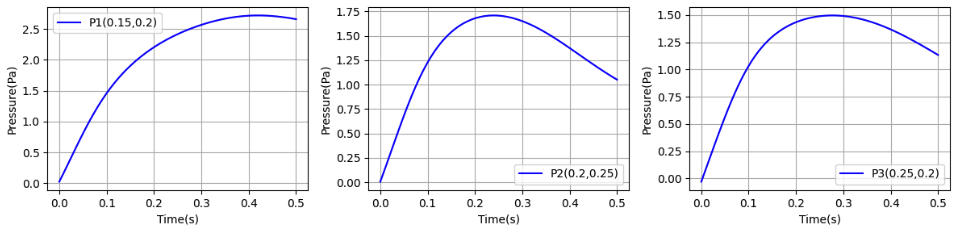
Pressure transition at the specific points
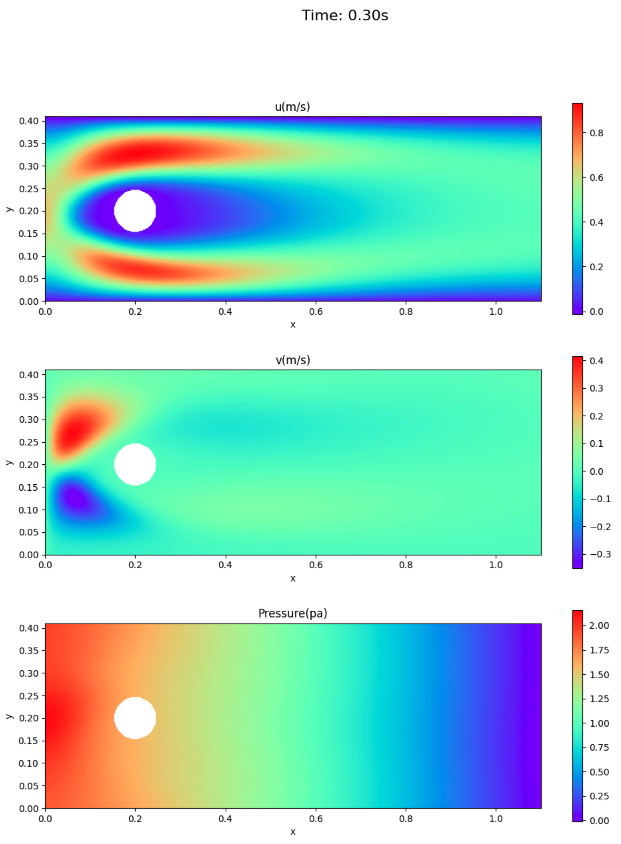
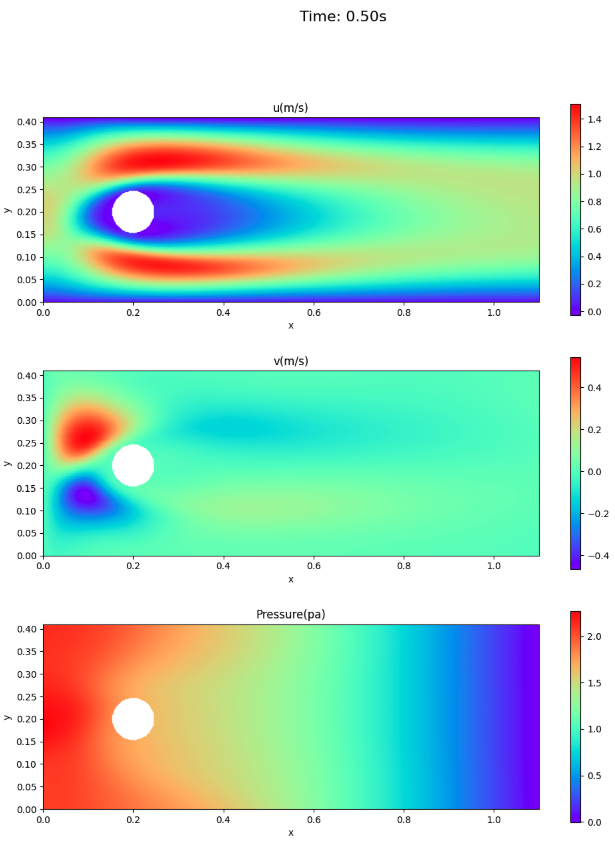
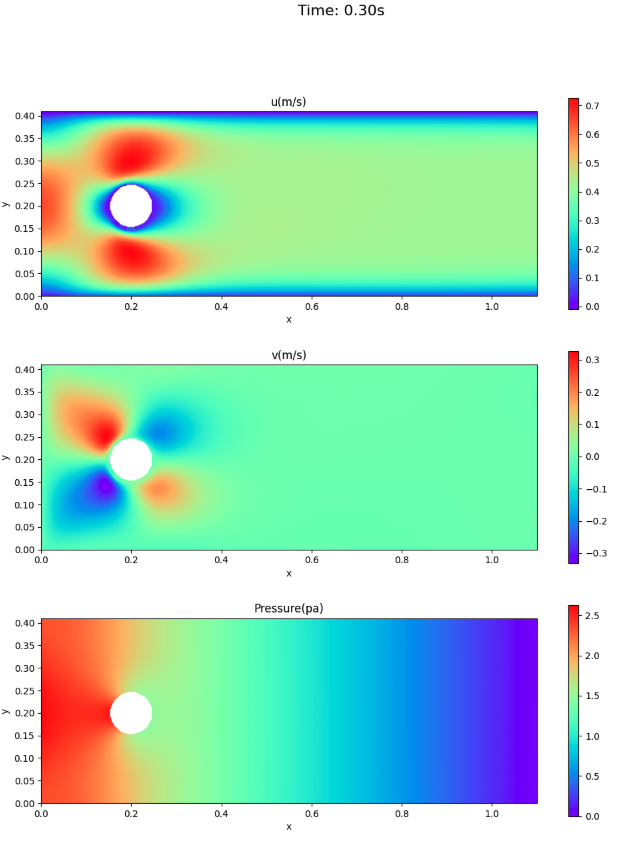
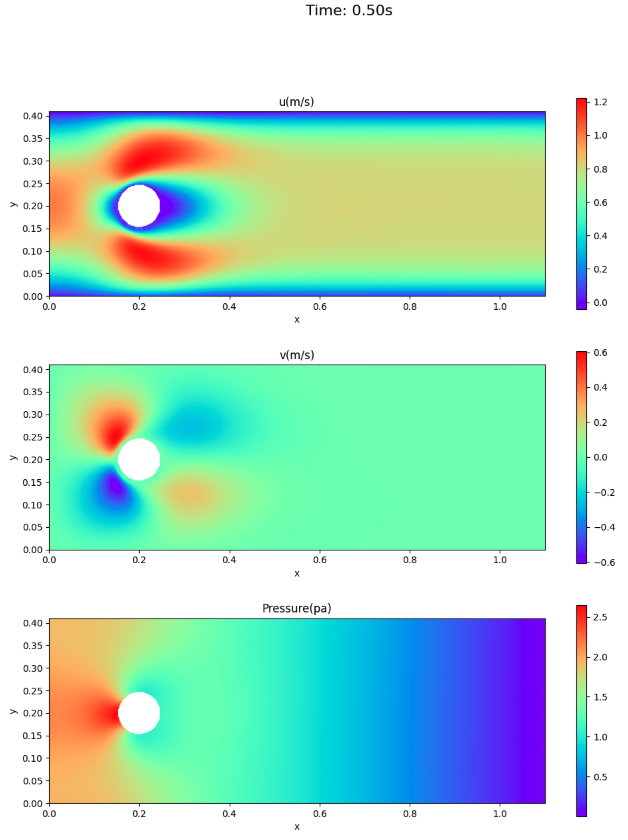
velocity and pressure fields
The velocity and pressure fields at times 0.3 and 0.5 seconds are shown here for comparison with the paper, not for animation.
Result with VP type
For reference, we also show the results with VP type (same code as the previous one except for learning rate, loss weighting, and 50,000 loops) under the same conditions (learning rate, loss weighting, and 50,000 loops).
Loss curves
Pressure transition at the specific points
velocity and pressure fields
Summary
Comparing both the ST and VP forms, I can qualitatively say the following
- ST form tends to converge losses more quickly.
- For the pressure at the three points, the curves of source 1. are different for both the ST and VP forms. The pressure does not return to near zero at 0.5 seconds. For the maximum value, the VP forms is closer to the value in Source 1.
- For the velocity field, the VP form is closer to the value of information source 1.
- Pressure remains in front of the cylinder at 0.5 seconds (end of one cycle).
I would like to change the learning rate and epoch (number of loops) and see the changes.
Also, when comparing the visualization results, you found that it is difficult to visually compare the results unless the scale of the display is aligned, so there is room for improvement in this area as well.