Introduction
Around this time last year, I spent two months working on a simulation of a two-dimensional cylindrical wake using PINNs. I hadn’t finished working on this article. This time, since I built a new Python development environment, I decided to tackle this theme as an example project, with Claude as my companion.
Code Generation
Prompt
I had Claude generate the source code using the following prompt.
Please generate PyTorch-based code to simulate the wake flow behind a two-dimensional cylinder using PINN.
Generated code
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from tqdm import tqdm
# デバイスの設定
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f"Using device: {device}")
# ニューラルネットワークの定義
class PINN(nn.Module):
def __init__(self, layers):
super(PINN, self).__init__()
self.layers = nn.ModuleList()
for i in range(len(layers) - 1):
self.layers.append(nn.Linear(layers[i], layers[i+1]))
def forward(self, x, y, t):
# 入力の正規化
inputs = torch.cat([x, y, t], dim=1)
for i in range(len(self.layers) - 1):
inputs = torch.tanh(self.layers[i](inputs))
# 最終層(活性化関数なし)
output = self.layers[-1](inputs)
# 速度と圧力を出力
u = output[:, 0:1] # x方向速度
v = output[:, 1:2] # y方向速度
p = output[:, 2:3] # 圧力
return u, v, p
# Navier-Stokes方程式の残差計算
class NavierStokesPINN:
def __init__(self, layers, Re=100):
self.model = PINN(layers).to(device)
self.Re = Re # レイノルズ数
self.nu = 1.0 / Re # 動粘性係数
# 最適化アルゴリズム
self.optimizer = torch.optim.Adam(self.model.parameters(), lr=1e-3)
self.scheduler = torch.optim.lr_scheduler.StepLR(
self.optimizer, step_size=5000, gamma=0.9
)
self.loss_history = []
def net_NS(self, x, y, t):
"""Navier-Stokes方程式の残差を計算"""
x.requires_grad_(True)
y.requires_grad_(True)
t.requires_grad_(True)
u, v, p = self.model(x, y, t)
# 1階微分
u_x = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u),
create_graph=True)[0]
u_y = torch.autograd.grad(u, y, grad_outputs=torch.ones_like(u),
create_graph=True)[0]
u_t = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u),
create_graph=True)[0]
v_x = torch.autograd.grad(v, x, grad_outputs=torch.ones_like(v),
create_graph=True)[0]
v_y = torch.autograd.grad(v, y, grad_outputs=torch.ones_like(v),
create_graph=True)[0]
v_t = torch.autograd.grad(v, t, grad_outputs=torch.ones_like(v),
create_graph=True)[0]
p_x = torch.autograd.grad(p, x, grad_outputs=torch.ones_like(p),
create_graph=True)[0]
p_y = torch.autograd.grad(p, y, grad_outputs=torch.ones_like(p),
create_graph=True)[0]
# 2階微分
u_xx = torch.autograd.grad(u_x, x, grad_outputs=torch.ones_like(u_x),
create_graph=True)[0]
u_yy = torch.autograd.grad(u_y, y, grad_outputs=torch.ones_like(u_y),
create_graph=True)[0]
v_xx = torch.autograd.grad(v_x, x, grad_outputs=torch.ones_like(v_x),
create_graph=True)[0]
v_yy = torch.autograd.grad(v_y, y, grad_outputs=torch.ones_like(v_y),
create_graph=True)[0]
# Navier-Stokes方程式(運動量保存則)
f_u = u_t + u * u_x + v * u_y + p_x - self.nu * (u_xx + u_yy)
f_v = v_t + u * v_x + v * v_y + p_y - self.nu * (v_xx + v_yy)
# 連続の式(質量保存則)
f_cont = u_x + v_y
return f_u, f_v, f_cont, u, v, p
def loss_function(self, x_domain, y_domain, t_domain,
x_inlet, y_inlet, t_inlet,
x_outlet, y_outlet, t_outlet,
x_wall_top, y_wall_top, t_wall_top,
x_wall_bottom, y_wall_bottom, t_wall_bottom,
x_cylinder, y_cylinder, t_cylinder,
x_init, y_init, t_init):
"""損失関数の計算"""
# 領域内でのNavier-Stokes方程式の残差
f_u, f_v, f_cont, _, _, _ = self.net_NS(x_domain, y_domain, t_domain)
loss_pde = torch.mean(f_u**2) + torch.mean(f_v**2) + torch.mean(f_cont**2)
# 入口境界条件(一様流)
u_inlet, v_inlet, _ = self.model(x_inlet, y_inlet, t_inlet)
loss_inlet = torch.mean((u_inlet - 1.0)**2) + torch.mean(v_inlet**2)
# 出口境界条件(圧力ゼロ、速度の勾配ゼロに近似)
u_outlet, v_outlet, p_outlet = self.model(x_outlet, y_outlet, t_outlet)
loss_outlet = torch.mean(p_outlet**2)
# 上下壁境界条件(自由滑り)
u_wall_t, v_wall_t, _ = self.model(x_wall_top, y_wall_top, t_wall_top)
u_wall_b, v_wall_b, _ = self.model(x_wall_bottom, y_wall_bottom, t_wall_bottom)
loss_wall = torch.mean(v_wall_t**2) + torch.mean(v_wall_b**2)
# 円柱表面境界条件(無滑り条件)
u_cyl, v_cyl, _ = self.model(x_cylinder, y_cylinder, t_cylinder)
loss_cylinder = torch.mean(u_cyl**2) + torch.mean(v_cyl**2)
# 初期条件
u_init, v_init, _ = self.model(x_init, y_init, t_init)
loss_init = torch.mean((u_init - 1.0)**2) + torch.mean(v_init**2)
# 総損失
loss = loss_pde + 10.0 * (loss_inlet + loss_outlet + loss_wall +
loss_cylinder + loss_init)
return loss, loss_pde, loss_inlet, loss_outlet, loss_wall, loss_cylinder
def train(self, epochs, x_domain, y_domain, t_domain,
x_inlet, y_inlet, t_inlet,
x_outlet, y_outlet, t_outlet,
x_wall_top, y_wall_top, t_wall_top,
x_wall_bottom, y_wall_bottom, t_wall_bottom,
x_cylinder, y_cylinder, t_cylinder,
x_init, y_init, t_init):
"""モデルの訓練"""
self.model.train()
pbar = tqdm(range(epochs), desc="Training")
for epoch in pbar:
self.optimizer.zero_grad()
loss, loss_pde, loss_inlet, loss_outlet, loss_wall, loss_cylinder = \
self.loss_function(x_domain, y_domain, t_domain,
x_inlet, y_inlet, t_inlet,
x_outlet, y_outlet, t_outlet,
x_wall_top, y_wall_top, t_wall_top,
x_wall_bottom, y_wall_bottom, t_wall_bottom,
x_cylinder, y_cylinder, t_cylinder,
x_init, y_init, t_init)
loss.backward()
self.optimizer.step()
self.scheduler.step()
self.loss_history.append(loss.item())
if epoch % 100 == 0:
pbar.set_postfix({
'Loss': f'{loss.item():.4e}',
'PDE': f'{loss_pde.item():.4e}',
'BC': f'{(loss_inlet + loss_outlet + loss_wall + loss_cylinder).item():.4e}'
})
def predict(self, x, y, t):
"""予測"""
self.model.eval()
with torch.no_grad():
u, v, p = self.model(x, y, t)
return u, v, p
# サンプリング点の生成
def generate_training_data(N_domain=5000, N_boundary=500, N_initial=1000):
"""訓練データの生成"""
# 計算領域の定義
x_min, x_max = -2.0, 10.0
y_min, y_max = -2.0, 2.0
t_min, t_max = 0.0, 5.0
# 円柱のパラメータ
x_cyl, y_cyl = 0.0, 0.0
r_cyl = 0.5
# 領域内のランダムサンプリング(円柱内部を除く)
x_domain = []
y_domain = []
t_domain = []
while len(x_domain) < N_domain:
x = np.random.uniform(x_min, x_max, N_domain * 2)
y = np.random.uniform(y_min, y_max, N_domain * 2)
t = np.random.uniform(t_min, t_max, N_domain * 2)
# 円柱内部を除外
mask = (x - x_cyl)**2 + (y - y_cyl)**2 > r_cyl**2
x = x[mask]
y = y[mask]
t = t[mask]
x_domain.extend(x[:N_domain - len(x_domain)])
y_domain.extend(y[:N_domain - len(y_domain)])
t_domain.extend(t[:N_domain - len(t_domain)])
x_domain = torch.FloatTensor(x_domain).reshape(-1, 1).to(device)
y_domain = torch.FloatTensor(y_domain).reshape(-1, 1).to(device)
t_domain = torch.FloatTensor(t_domain).reshape(-1, 1).to(device)
# 入口境界(x = x_min)
x_inlet = torch.ones(N_boundary, 1).to(device) * x_min
y_inlet = torch.FloatTensor(np.random.uniform(y_min, y_max, N_boundary)).reshape(-1, 1).to(device)
t_inlet = torch.FloatTensor(np.random.uniform(t_min, t_max, N_boundary)).reshape(-1, 1).to(device)
# 出口境界(x = x_max)
x_outlet = torch.ones(N_boundary, 1).to(device) * x_max
y_outlet = torch.FloatTensor(np.random.uniform(y_min, y_max, N_boundary)).reshape(-1, 1).to(device)
t_outlet = torch.FloatTensor(np.random.uniform(t_min, t_max, N_boundary)).reshape(-1, 1).to(device)
# 上壁境界(y = y_max)
x_wall_top = torch.FloatTensor(np.random.uniform(x_min, x_max, N_boundary)).reshape(-1, 1).to(device)
y_wall_top = torch.ones(N_boundary, 1).to(device) * y_max
t_wall_top = torch.FloatTensor(np.random.uniform(t_min, t_max, N_boundary)).reshape(-1, 1).to(device)
# 下壁境界(y = y_min)
x_wall_bottom = torch.FloatTensor(np.random.uniform(x_min, x_max, N_boundary)).reshape(-1, 1).to(device)
y_wall_bottom = torch.ones(N_boundary, 1).to(device) * y_min
t_wall_bottom = torch.FloatTensor(np.random.uniform(t_min, t_max, N_boundary)).reshape(-1, 1).to(device)
# 円柱表面境界
theta = np.random.uniform(0, 2*np.pi, N_boundary)
x_cylinder = torch.FloatTensor(x_cyl + r_cyl * np.cos(theta)).reshape(-1, 1).to(device)
y_cylinder = torch.FloatTensor(y_cyl + r_cyl * np.sin(theta)).reshape(-1, 1).to(device)
t_cylinder = torch.FloatTensor(np.random.uniform(t_min, t_max, N_boundary)).reshape(-1, 1).to(device)
# 初期条件(t = 0)
x_init = []
y_init = []
while len(x_init) < N_initial:
x = np.random.uniform(x_min, x_max, N_initial * 2)
y = np.random.uniform(y_min, y_max, N_initial * 2)
mask = (x - x_cyl)**2 + (y - y_cyl)**2 > r_cyl**2
x = x[mask]
y = y[mask]
x_init.extend(x[:N_initial - len(x_init)])
y_init.extend(y[:N_initial - len(y_init)])
x_init = torch.FloatTensor(x_init).reshape(-1, 1).to(device)
y_init = torch.FloatTensor(y_init).reshape(-1, 1).to(device)
t_init = torch.zeros(N_initial, 1).to(device)
return (x_domain, y_domain, t_domain,
x_inlet, y_inlet, t_inlet,
x_outlet, y_outlet, t_outlet,
x_wall_top, y_wall_top, t_wall_top,
x_wall_bottom, y_wall_bottom, t_wall_bottom,
x_cylinder, y_cylinder, t_cylinder,
x_init, y_init, t_init)
# 可視化
def visualize_flow(pinn, t_value=2.0, save_path='flow_field.png'):
"""流れ場の可視化"""
x = np.linspace(-2, 10, 150)
y = np.linspace(-2, 2, 80)
X, Y = np.meshgrid(x, y)
x_flat = torch.FloatTensor(X.flatten()).reshape(-1, 1).to(device)
y_flat = torch.FloatTensor(Y.flatten()).reshape(-1, 1).to(device)
t_flat = torch.ones_like(x_flat) * t_value
u, v, p = pinn.predict(x_flat, y_flat, t_flat)
u = u.cpu().numpy().reshape(X.shape)
v = v.cpu().numpy().reshape(X.shape)
p = p.cpu().numpy().reshape(X.shape)
# 円柱内部をマスク
mask = (X - 0.0)**2 + (Y - 0.0)**2 < 0.5**2
u[mask] = np.nan
v[mask] = np.nan
p[mask] = np.nan
# 速度の大きさ
velocity_magnitude = np.sqrt(u**2 + v**2)
fig, axes = plt.subplots(2, 2, figsize=(16, 8))
# u速度
im1 = axes[0, 0].contourf(X, Y, u, levels=20, cmap='RdBu_r')
axes[0, 0].set_title(f'u-velocity at t={t_value}')
axes[0, 0].set_xlabel('x')
axes[0, 0].set_ylabel('y')
axes[0, 0].add_patch(plt.Circle((0, 0), 0.5, color='black'))
plt.colorbar(im1, ax=axes[0, 0])
# v速度
im2 = axes[0, 1].contourf(X, Y, v, levels=20, cmap='RdBu_r')
axes[0, 1].set_title(f'v-velocity at t={t_value}')
axes[0, 1].set_xlabel('x')
axes[0, 1].set_ylabel('y')
axes[0, 1].add_patch(plt.Circle((0, 0), 0.5, color='black'))
plt.colorbar(im2, ax=axes[0, 1])
# 圧力
im3 = axes[1, 0].contourf(X, Y, p, levels=20, cmap='RdBu_r')
axes[1, 0].set_title(f'Pressure at t={t_value}')
axes[1, 0].set_xlabel('x')
axes[1, 0].set_ylabel('y')
axes[1, 0].add_patch(plt.Circle((0, 0), 0.5, color='black'))
plt.colorbar(im3, ax=axes[1, 0])
# 速度の大きさとストリームライン
im4 = axes[1, 1].contourf(X, Y, velocity_magnitude, levels=20, cmap='viridis')
axes[1, 1].streamplot(X, Y, u, v, color='white', linewidth=0.5, density=1.5)
axes[1, 1].set_title(f'Velocity magnitude at t={t_value}')
axes[1, 1].set_xlabel('x')
axes[1, 1].set_ylabel('y')
axes[1, 1].add_patch(plt.Circle((0, 0), 0.5, color='black'))
plt.colorbar(im4, ax=axes[1, 1])
plt.tight_layout()
plt.savefig(save_path, dpi=150, bbox_inches='tight')
plt.show()
print(f"Flow field visualization saved to {save_path}")
def plot_loss_history(pinn, save_path='loss_history.png'):
"""損失関数の履歴をプロット"""
plt.figure(figsize=(10, 6))
plt.plot(pinn.loss_history)
plt.yscale('log')
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Training Loss History')
plt.grid(True)
plt.savefig(save_path, dpi=150, bbox_inches='tight')
plt.show()
print(f"Loss history plot saved to {save_path}")
# メイン実行
if __name__ == "__main__":
# ハイパーパラメータ
layers = [3, 64, 64, 64, 64, 3] # [入力層, 隠れ層..., 出力層]
Re = 100 # レイノルズ数
epochs = 10000 # 訓練エポック数
print("=" * 60)
print("2D Cylinder Flow Simulation using PINN")
print("=" * 60)
print(f"Reynolds number: {Re}")
print(f"Network architecture: {layers}")
print(f"Training epochs: {epochs}")
print("=" * 60)
# PINNモデルの初期化
pinn = NavierStokesPINN(layers, Re=Re)
# 訓練データの生成
print("\nGenerating training data...")
training_data = generate_training_data(
N_domain=5000,
N_boundary=500,
N_initial=1000
)
# モデルの訓練
print("\nStarting training...")
pinn.train(epochs, *training_data)
# 損失関数の履歴をプロット
print("\nPlotting loss history...")
plot_loss_history(pinn, save_path='/workspace/outputs/loss_history.png')
# 流れ場の可視化(複数の時刻)
print("\nVisualizing flow fields...")
for t in [0.5, 1.0, 2.0, 3.0]:
visualize_flow(pinn, t_value=t,
save_path=f'/workspace/outputs/flow_field_t{t:.1f}.png')
# モデルの保存
torch.save(pinn.model.state_dict(), '/workspace/outputs/pinn_cylinder_model.pth')
print("\nModel saved to /workspace/outputs/pinn_cylinder_model.pth")
print("\n" + "=" * 60)
print("Simulation completed!")
print("=" * 60)
Execution results
Error History
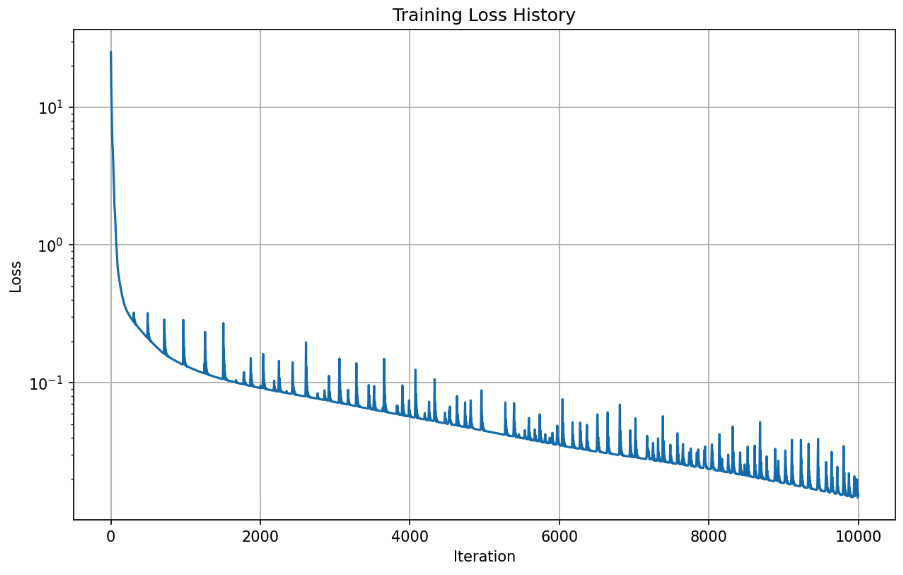
Visualization
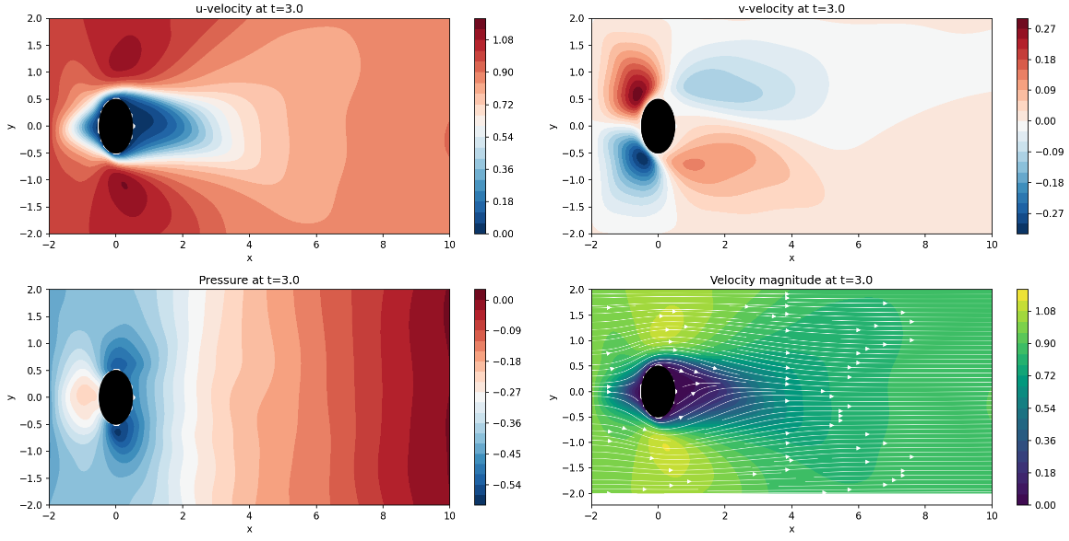
Summary
I’m surprised results came so easily. It makes last year’s hard work feel wasted. Well, I suppose last year’s experience was a learning opportunity.
I want to analyze the generated code a bit more.