はじめに
この記事に引き続き、JDLA E資格のシラバスの範囲をまとめたもので、今回は「機械学習」に関するもの。
参考文献
機械学習に関して、自分が使っている参考図書は次の通り。
- 機械学習のエッセンス 加藤公一 著 SBクリエイティブ
→ 教材ビデオの講師が紹介していた。 - Pythonによるデータ分析の教科書 寺田学・辻真吾・鈴木たかのり・福島真太郎 著 翔泳社
→ Python3エンジニア認定データ分析試験を受講する際に購入、学習した。 - 東京大学のデータサイエンティスト育成講座 塚本邦尊・山田典一・大澤文孝 著 マイナビ出版
→ 前回の記事でも紹介した書籍。 今回はChapter 8、9を参照した。
線形回帰モデル
回帰問題
線形回帰モデルとは、回帰問題(離散あるいは連続値からなる入力するから連続値の出力)を予測する教師あり学習の手法である。
入力データ(説明変数)が1次元の場合を単回帰モデルと言い、多次元の場合を線形重回帰モデルという。幾何学的には、単回帰は直線で表され、重回帰は曲面で表される。
入力ベクトルと未知のパラメータの各要素を掛け・足し合わせた(線型結合;入力とパラメータの内積)もので、表現できる。すなわち次のような目的関数で表される。 $$ y = w_0+ w_1x_1+w_2x_2+ \cdots + w_mx_m $$ ここで、$y$は目的変数、$w_i$は回帰係数、$x_i$は説明変数と呼ばれる。
上記の目的関数は、次の行列表現でも表される。 $$ \boldsymbol{y} = \boldsymbol{X}\boldsymbol{w} $$ ここで、$\boldsymbol{x_i} = (1, x_{i1},\cdots,x_{im})^{T}$、$\boldsymbol{y} =(y_1,y_2,\cdots,y_n)^T$、$\boldsymbol{X} =(\boldsymbol{x}_1,\cdots,\boldsymbol{x}_n)^T$、$\boldsymbol{w} =(w_0, w_1,\cdots,w_m)^T$である。$m$は説明変数の数、$n$は入力データ数である。
ハンズオン(ボストン住宅価格の予測)
# 線形回帰モデルのハンズオン
# scit-learnでデータを読み込む
# pandasのデータフレームを使用する
from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np
boston = load_boston()
df = DataFrame(data=boston.data, columns=boston.feature_names)
df['PRICE'] = np.array(boston.target)
# 説明変数
data2 = df.loc[:,['CRIM','RM']].values
# 目的変数
target = df.loc[:,'PRICE'].values
# sklearnのLinearRegressionを使う
from sklearn.linear_model import LinearRegression
# 線形回帰モデルを取得
model = LinearRegression()
# 学習
model.fit(data2, target)
# sklearnのLinearRegressionを使う
from sklearn.linear_model import LinearRegression
# 線形回帰モデルを取得
model = LinearRegression()
# 学習
model.fit(data2, target)
結果は、次の通り。
array([4.24007956])
結果に対する考察
説明変数は、犯罪率と部屋数の2つであり、とちらがより価格に効いているか以下で確認した。
# 犯罪率:0.3で固定して、部屋数を変えてみる。
print("犯罪率:0.3、部屋数:3、価格:{}".format(model.predict([[0.3,3]])))
print("犯罪率:0.3、部屋数:4、価格:{}".format(model.predict([[0.3,4]])))
print("犯罪率:0.3、部屋数:5、価格:{}".format(model.predict([[0.3,5]])))
print("犯罪率:0.3、部屋数:6、価格:{}".format(model.predict([[0.3,6]])))
print("犯罪率:0.3、部屋数:7、価格:{}".format(model.predict([[0.3,7]])))
print("犯罪率:0.3、部屋数:8、価格:{}".format(model.predict([[0.3,8]])))
print("\n")
# 部屋数:4で固定して、犯罪率を変えてみる。
print("犯罪率:0.1、部屋数:4、価格:{}".format(model.predict([[0.1,4]])))
print("犯罪率:0.2、部屋数:4、価格:{}".format(model.predict([[0.2,4]])))
print("犯罪率:0.3、部屋数:4、価格:{}".format(model.predict([[0.3,4]])))
print("犯罪率:0.4、部屋数:4、価格:{}".format(model.predict([[0.4,4]])))
print("犯罪率:0.5、部屋数:4、価格:{}".format(model.predict([[0.5,4]])))
print("犯罪率:0.6、部屋数:4、価格:{}".format(model.predict([[0.4,4]])))
結果は、次の通り、部屋数が価格への寄与度が大である。
犯罪率:0.3、部屋数:3、価格:[-4.15098869]
犯罪率:0.3、部屋数:4、価格:[4.24007956]
犯罪率:0.3、部屋数:5、価格:[12.6311478]
犯罪率:0.3、部屋数:6、価格:[21.02221605]
犯罪率:0.3、部屋数:7、価格:[29.4132843]
犯罪率:0.3、部屋数:8、価格:[37.80435254]
犯罪率:0.1、部屋数:4、価格:[4.29306221]
犯罪率:0.2、部屋数:4、価格:[4.26657088]
犯罪率:0.3、部屋数:4、価格:[4.24007956]
犯罪率:0.4、部屋数:4、価格:[4.21358823]
犯罪率:0.5、部屋数:4、価格:[4.18709691]
犯罪率:0.6、部屋数:4、価格:[4.21358823]
図を使って上記を表す。以下がそのコード。
# 図を使ってみる
import matplotlib.pyplot as plt
fig, axes = plt.subplots(ncols=2)# 2つのサブプロットで描画する
axes[0].scatter(df[['RM']], df[['PRICE']], c='blue', marker = 'o')
axes[0].set_xlabel('Rooms')
axes[0].set_ylabel('Price')
axes[1].scatter(df[['CRIM']], df[['PRICE']], c='blue', marker = 'x')
axes[1].set_xlabel('Crimes')
axes[1].set_ylabel('Price')
実行結果は、次の通り。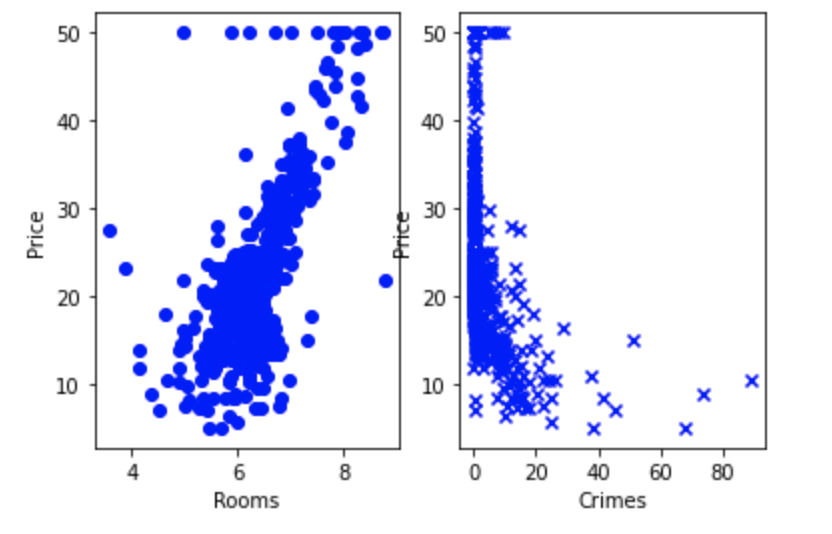
非線形回帰モデル
非線形回帰
データの構造を線形で捉えられるケースは限られており、データが複雑な分布をもつ現象に対しては、非線形回帰モデルを用いる。そのために、回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線形結合が用いられる。次のように表現できる。 $$ y_i = w_0 + \sum_{j=1}^m w_j \phi(\boldsymbol{x}_i) $$ ここで、$\phi()$が基底関数である。基底関数としては、多項式関数、ガウス型基底関数、スプライン関数などがある。
非線形モデルは、線形モデルより高い表現能力を持った予測が行える。しかしながら高い表現能力を持つモデルは、訓練データに過度に適用し、未知のデータに対して適用しない、いわゆる汎化性能が低下する問題が発生する。(過学習という、訓練誤差小・汎化誤差大の状況に陥る)
テスト手法
機械学習においては、モデルの精度は、テスト誤差で評価することが大事である。そのため、テストデータを確保し、汎化性能を評価するため、ホールドアウト法、クロスバリデーション(交差検証)などの方法がある。
k分割交差検証(k-fold cross varidation)は、全データを$k$個に分割し、学習も$k$回繰り返す。$i$回目の学習時に$i$番目のサブセットをテストデータとし、残りの$(k-1)$個のサブセットを学習データとして使う手法です。
正則化
訓練データに過度に適用し、未知のデータに適用しないという問題を適切に制御(モデルの複雑さを制御)するための仕組みを正則化という。正則化法(罰則化法)は、モデルの複雑さに伴って、その値が大きくなる正則化項を課した関数を最小化する手法である。
正則化項としてL2ノルムを用いるリッジ回帰、L1ノルムを用いるラッソ回帰とがある。
リッジ回帰においては、正則化係数を十分に大きくすると、いくつかの回帰係数は$0$に近づくが、完全に$0$とはならない。一方、ラッソ回帰においては、正則化係数を十分に大きくすると、いくつかの回帰係数は完全に$0$となる。
実装演習用コードを使っての考察
実装演習用のコード「skl_nonlinear regression.ipynb」を使った実行とその評価を以下に述べる。次の図は、KernelRidgeで擬似的に作成したデータから学習した結果のグラフである。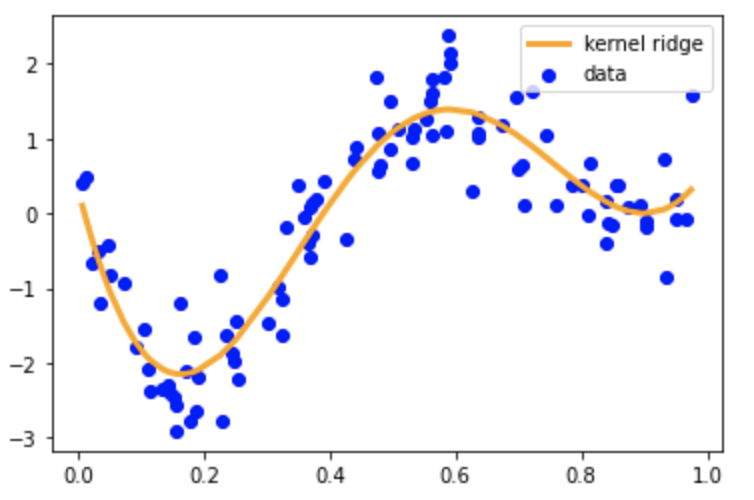
次に多項式モデルで、上記のデータ(図で青色の点)を予測した結果。但し、1次式(線形)および4次式での予測結果である。4次以上は、4次式の結果とほぼ等しかった。
次のコードの通り、次数をのリストを変更した。
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
#PolynomialFeatures(degree=1)
#deg = [1,2,3,4,5,6,7,8,9,10]
deg = [1,4]
for d in deg:
regr = Pipeline([
('poly', PolynomialFeatures(degree=d)),
('linear', LinearRegression())
])
regr.fit(data, target)
# make predictions
p_poly = regr.predict(data)
# plot regression result
plt.scatter(data, target, label='data')
plt.plot(data, p_poly, label='polynomial of degree %d' % (d))
上記の結果のグラフは、以下の通りである。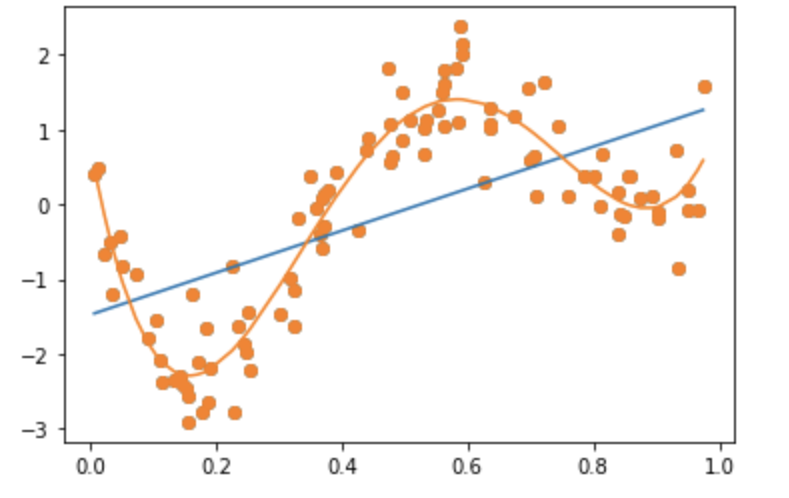
上記2つのグラフを比較して分かる通り、KernelRidgeでのモデルは、4次式で与えられるデータを上手く予測していることが分かる。
ロジスティック回帰モデル
ロジスティック回帰
ロジスティック回帰は、「回帰」との名前ではあるが、分類問題に適用されるアルゴリズムである。ロジスティック回帰では、ラベルの値が2種類($0$または$1$の2つ)しかないような教師あり訓練データに適用される。
与えられた特徴量のサンプル$\boldsymbol{x}\in \mathbb{R}^d$に対して、ラベル$y$が$1$になる確率を$P(Y=1|X=\boldsymbol{x})$で表し、ラベル$y$が$0$になる確率を$P(Y=0|X=\boldsymbol{x})$で表す。ロジスティック回帰は、次の式で表される。 $$ P(Y=1|X=\boldsymbol{x})=\sigma(w_0 + \sum_{j=1}^{d} x_j W_j) = \sigma(\boldsymbol{w}^T \boldsymbol{x}^T) $$ ここで、$\sigma$はシグモイド関数で、次のように表される。 $$ \sigma(x) = \frac{1}{1+\exp (-ax)} $$ シグモイド関数の微分は、シグモイド関数自身で表現することが可能である。 $$ \begin{align} \frac{\partial \sigma(x)}{\partial x} &= \frac{\partial}{\partial x}\left(\frac{1}{1+\exp (-ax)} \right) \\ &= a \sigma(x)(1-\sigma(x)) \end{align} $$
シグモイド関数は、任意の$\xi$に対して、$0<\sigma(\xi)<1$であり、$\lim_{\xi\to-\infty}=0$、$\lim_{\xi\to\infty}=1$が成り立つ。この性質のため、シグモイド関数は確率として扱えるようになる。
分類問題では、ラベルは$1$か$0$なので、$0$になる確率は$P(Y=0|X=\boldsymbol{x}) = 1 - P(Y=1|X=\boldsymbol{x})$となる。以上をまとめる、ラベルの値が$y$になる確率は次のようになる。 $$ \begin{align} P(Y=y|X=\boldsymbol{x}) &= P(Y=1|X=\boldsymbol{x})^{y}P(Y=0|X=\boldsymbol{x})^{1-y} \\ &= \sigma(\boldsymbol{x}^T\boldsymbol{w})^y (1-\sigma(\boldsymbol{X}^T \boldsymbol{w}))^{1-y} \end{align} $$ 上式に$y=1$を代入すると$P(Y=1|X=\boldsymbol{x})=\sigma(\boldsymbol{x}^T\boldsymbol{w})$となり、$y=0$を代入すると$P(Y=0|X=\boldsymbol{x})=1-\sigma(\boldsymbol{x}^T \boldsymbol{w})$となる。
モデルの評価
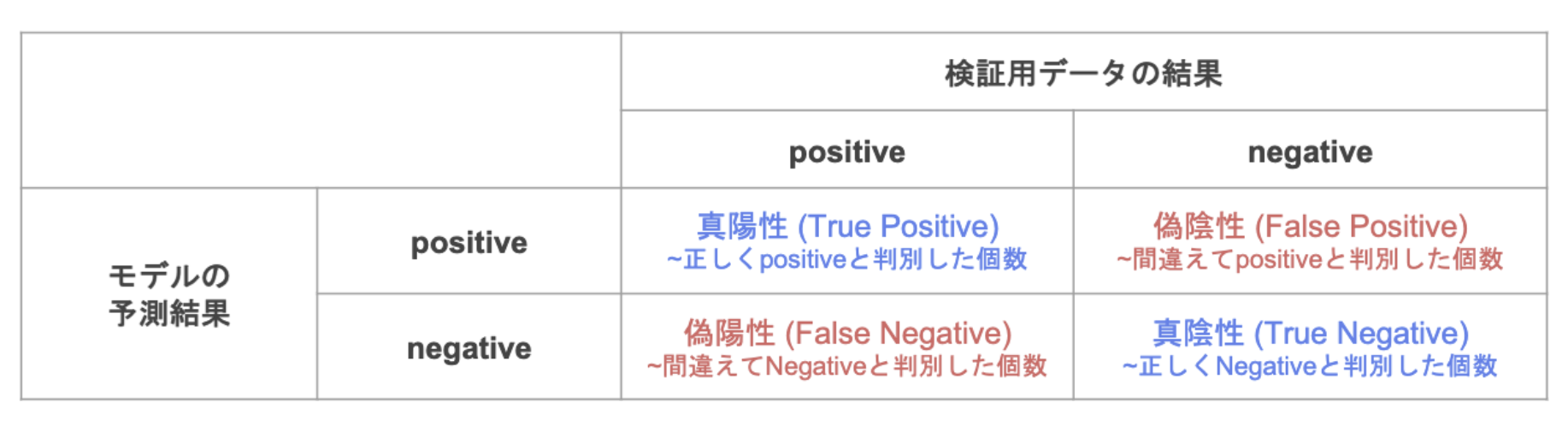
分類問題でのモデルの良し悪しを判断する指標として、適合率(precision)、再現率(recall)、F値(F-Value)、正解率(accuracy)などがある。これらは、以下の混同行列(confusion matrix)から計算できる。
 $$
\begin{align}
適合率&=\frac{TP}{TP+FP} \\
再現率&=\frac{TP}{TP+FN} \\
正解率&=\frac{TP+TN}{TP+FN+FP+TN}
\end{align}
$$
$$
\begin{align}
適合率&=\frac{TP}{TP+FP} \\
再現率&=\frac{TP}{TP+FN} \\
正解率&=\frac{TP+TN}{TP+FN+FP+TN}
\end{align}
$$
ハンズオン(タイタニック)
課題は、次の通り。「年齢が30歳で、男の乗客は生き残れるか?」
タイタニックのデータを読み込み、年齢(Age)がnullの時は、中央値で補間し、特徴量を年齢と性別とし、生き残ったか(Survived)でロジスティック回帰モデルを学習する。学習結果で30歳、男性で生き残る確率を求めた。
# ロジスティック回帰:ハンズオン(タイタニック)
# 30歳男性の生存は?
import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
# タイタニックのデータ(csv)を読み込む
titanic_df = pd.read_csv('study_ai_ml_google/data/titanic_train.csv')
# 予測に不要と思われるカラムをドロップ
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
# Ageカラムのnullを中央値で補間
titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())
# 文字列の性別を数値化し、Genderカラムに格納
titanic_df['Gender'] = titanic_df['Sex'].map({'female': 0, 'male': 1}).astype(int)
# 年齢と性別のリストを作成
data = titanic_df.loc[:,['AgeFill','Gender']].values
# 生死フラグのみのリストを作成
label = titanic_df.loc[:,['Survived']].values
# ロジスティック回帰のモデルを作成
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
# 学習
model.fit(data, label)
# 30歳、男性の生存確率は?
model.predict_proba([[30,1]])
結果は、次の通りとなった。
array([[0.80668102, 0.19331898]])
30歳男性が生き残る確率は、19%である。
考察
次に、サンプルを参考にしながら、実際に動かして、結果を確かめてみた。
先ず、タイタニックデータから、特徴量の性別+階級(社会階級で、1:high/2:middle/3:low)を合わせた特徴量と年齢(nullは中央値で補間)の2軸で生死をグラフ化する。
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
# タイタニックのデータ(csv)を読み込む
titanic_df = pd.read_csv('study_ai_ml_google/data/titanic_train.csv')
# 予測に不要と思われるカラムをドロップ
titanic_df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
# Ageカラムのnullを中央値で補間
titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())
# 文字列の性別を数値化し、Genderカラムに格納
titanic_df['Gender'] = titanic_df['Sex'].map({'female': 0, 'male': 1}).astype(int)
# Pclass(階級)とGender(性別)の特徴量を合わせたものを、 Pclass_Gender特徴量とする。
titanic_df['Pclass_Gender'] = titanic_df['Pclass'] + titanic_df['Gender']
np.random.seed = 0
xmin, xmax = -5, 85
ymin, ymax = 0.5, 4.5
index_survived = titanic_df[titanic_df["Survived"]==0].index
index_notsurvived = titanic_df[titanic_df["Survived"]==1].index
from matplotlib.colors import ListedColormap
fig, ax = plt.subplots()
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
sc = ax.scatter(titanic_df.loc[index_survived, 'AgeFill'],
titanic_df.loc[index_survived, 'Pclass_Gender']+(np.random.rand(len(index_survived))-0.5)*0.1,
color='r', label='Not Survived', alpha=0.3)
sc = ax.scatter(titanic_df.loc[index_notsurvived, 'AgeFill'],
titanic_df.loc[index_notsurvived, 'Pclass_Gender']+(np.random.rand(len(index_notsurvived))-0.5)*0.1,
color='b', label='Survived', alpha=0.3)
ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass_Gender')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.legend(bbox_to_anchor=(1.4, 1.03))
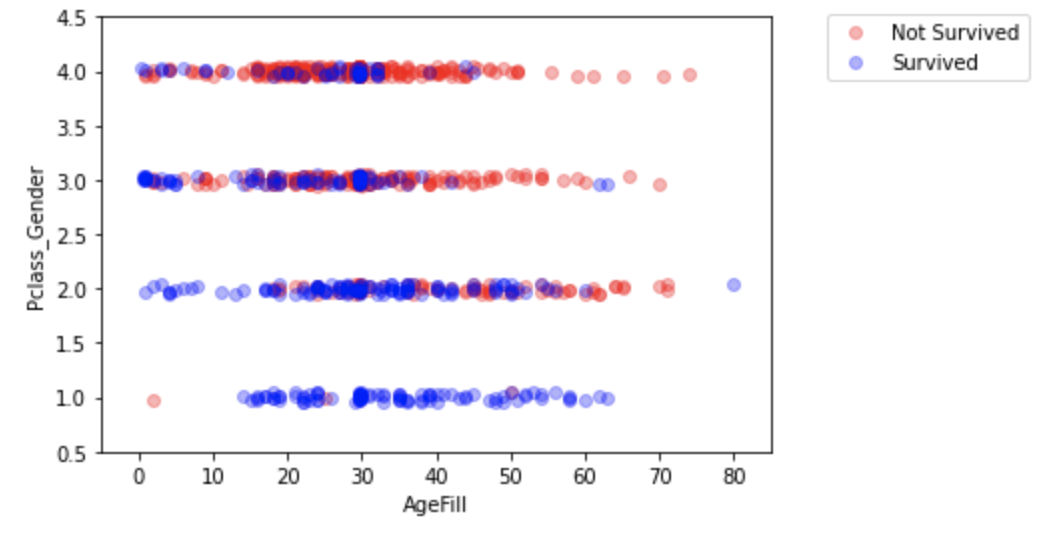
等級+性別と年齢の特徴量を使って学習し、結果を同じくグラフ化する。
# Pclass_Gender(階級+性別)とAgeFill(補間した年齢)のリスト作成
data2 = titanic_df.loc[:, ["AgeFill", "Pclass_Gender"]].values
# 生死フラグのみのリストを作成
label2 = titanic_df.loc[:,["Survived"]].values
# ロジスティック回帰のモデルを作成
from sklearn.linear_model import LogisticRegression
model2 = LogisticRegression()
# 学習
model2.fit(data2, label2)
h = 0.02
xmin, xmax = -5, 85
ymin, ymax = 0.5, 4.5
xx, yy = np.meshgrid(np.arange(xmin, xmax, h), np.arange(ymin, ymax, h))
Z = model2.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z = Z.reshape(xx.shape)
fig, ax = plt.subplots()
levels = np.linspace(0, 1.0)
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
#contour = ax.contourf(xx, yy, Z, cmap=cm, levels=levels, alpha=0.5)
sc = ax.scatter(titanic_df.loc[index_survived, 'AgeFill'],
titanic_df.loc[index_survived, 'Pclass_Gender']+(np.random.rand(len(index_survived))-0.5)*0.1,
color='r', label='Not Survived', alpha=0.3)
sc = ax.scatter(titanic_df.loc[index_notsurvived, 'AgeFill'],
titanic_df.loc[index_notsurvived, 'Pclass_Gender']+(np.random.rand(len(index_notsurvived))-0.5)*0.1,
color='b', label='Survived', alpha=0.3)
ax.set_xlabel('AgeFill')
ax.set_ylabel('Pclass_Gender')
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
#fig.colorbar(contour)
x1 = xmin
x2 = xmax
y1 = -1*(model2.intercept_[0]+model2.coef_[0][0]*xmin)/model2.coef_[0][1]
y2 = -1*(model2.intercept_[0]+model2.coef_[0][0]*xmax)/model2.coef_[0][1]
ax.plot([x1, x2] ,[y1, y2], 'k--')
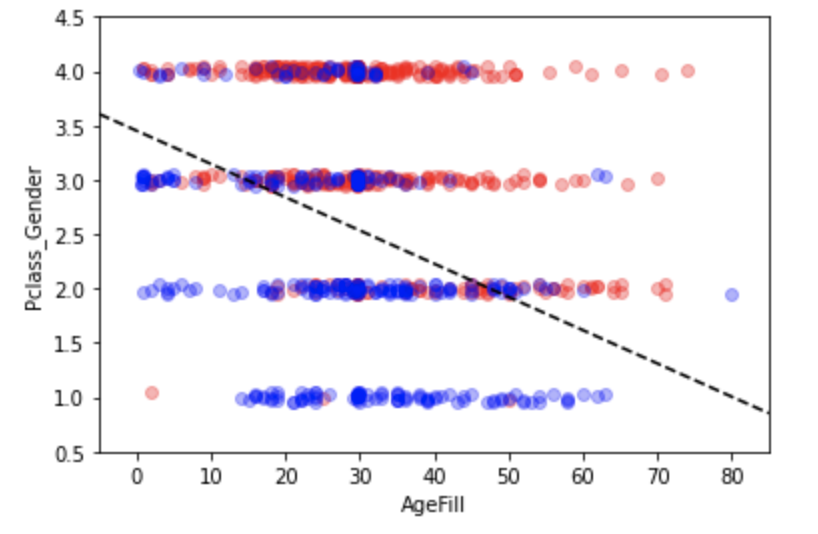
上記の結果、年齢が高く、階級が低い程( Pclassの値は大きくなる)、死亡する割合が多くなる傾向となることが判る。
主成分分析
主成分分析(Principal Component Analysis; PCA)は、教師なし学習の一種であり、次元圧縮の手法である。PCAにより多変量データを持つ構造をより少数個の指標に圧縮する。圧縮された少数の変数を利用した分析に使われたり、2、3の変数に圧縮することで、可視化(2次元、3次元)に使われる。
PCAは与えられたデータをより低次元の空間に射影し、射影後の点の散らばりができるだけ大きくなるようにする。すなわち、情報損失が小さくなるように、分散が最大になる方向に射影すれよい。
第一主成分は、データの共分散行列の最大固有値を与える固有ベクトルである。すなわち、主成分問題=固有値問題となる。
ハンズオン(乳がん検査データ)
まずは、データを読み込む。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# 乳がん検査データを読み込む
cancer_df = pd.read_csv('study_ai_ml_google/data/cancer.csv')
# データの個数と次元数を確認
print('cancer df shape: {}'.format(cancer_df.shape))
cancer_df.drop('Unnamed: 32', axis=1, inplace=True)
cancer_df
print('cancer df shape: {}'.format(cancer_df.shape))
読み込んだデータのレコード数と次元(カラム数)
cancer df shape: (569, 33)
cancer df shape: (569, 32)
ロジスティック回帰で学習し、学習データ、テストデータでの精度、および混同行列を出力する。
# 目的変数の抽出
y = cancer_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0)
# 説明変数の抽出
X = cancer_df.loc[:, 'radius_mean':]
# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# ロジスティック回帰で学習
logistic = LogisticRegressionCV(cv=10, random_state=0)
logistic.fit(X_train_scaled, y_train)
# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))
検証結果は、以下の通り。テストデータで97%の精度で分類できている。
Train score: 0.988
Test score: 0.972
Confustion matrix:
[[89 1]
[ 3 50]]
pca = PCA(n_components=30)
pca.fit(X_train_scaled)
plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)
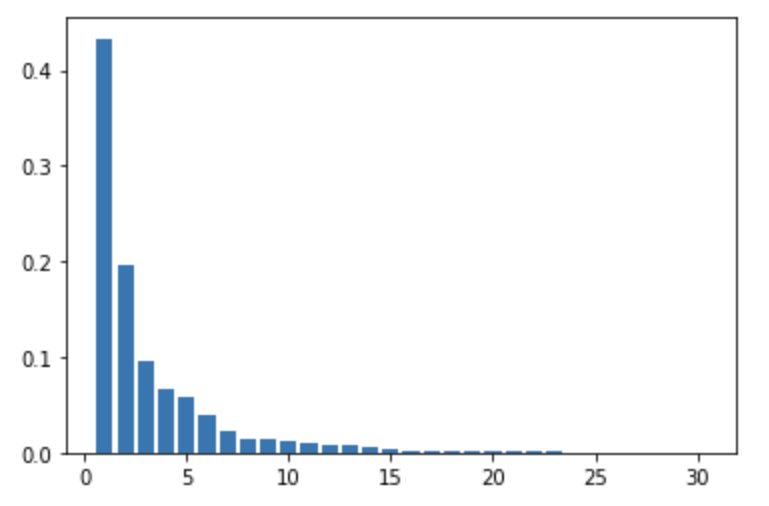
# PCA
# 次元数2まで圧縮
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
print('X_train_pca shape: {}'.format(X_train_pca.shape))
# X_train_pca shape: (426, 2)
# 寄与率
print('explained variance ratio: {}'.format(pca.explained_variance_ratio_))
# explained variance ratio: [ 0.43315126 0.19586506]
# 散布図にプロット
temp = pd.DataFrame(X_train_pca)
temp['Outcome'] = y_train.values
b = temp[temp['Outcome'] == 0]
m = temp[temp['Outcome'] == 1]
plt.scatter(x=b[0], y=b[1], marker='o') # 良性は○でマーク
plt.scatter(x=m[0], y=m[1], marker='^') # 悪性は△でマーク
plt.xlabel('PC 1') # 第1主成分をx軸
plt.ylabel('PC 2') # 第2主成分をy軸
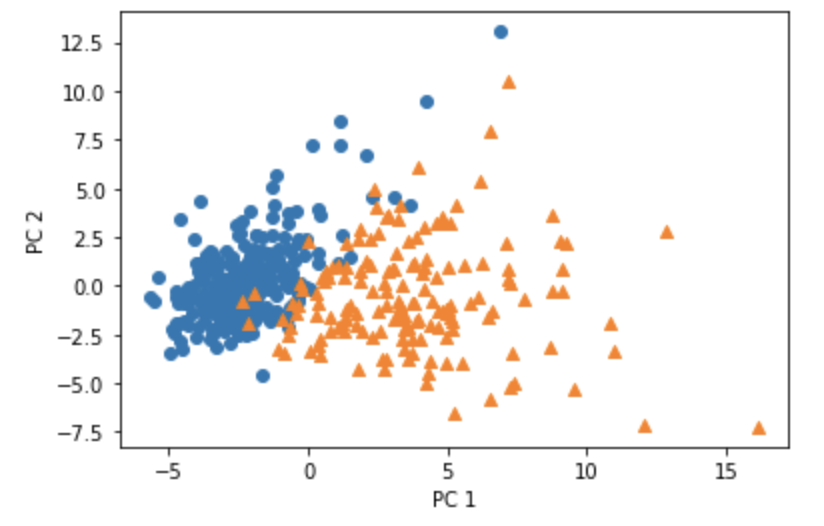
このコードの出力結果は、次の通り。第1成分の寄与度が0.433、第2成分の寄与度が0.196である。
X_train_pca shape: (426, 2)
explained variance ratio: [0.43315126 0.19586506]
アルゴリズム
この章では、k近傍法(k-nearest neighbor algorithm; k-NN)とk平均法(k-means clustering)とを説明する。冒頭に"k"がついて混同しがちであるが、k近傍法は、教師ありの分類のためのアルゴリズムであり、k平均法は、教師なしのクラスタリングのアルゴリズムである。
k近傍法(kNN)
与えられた学習データをベクトル空間上にプロットしておき、未知のデータが得られたら、そこから距離が近い順に任意のk個を取得し、その多数決でデータが属するクラスを推定するというもの。 分類のアルゴリズムの中でも、シンプルでわかりやすいアルゴリズムである。
kを変化させると結果も変わる。また、kを大きくすると決定境界は滑らかになる。特にkが1の時を最近傍法ともいう。
k平均法(k-means)
与えられたデータをk個のクラスタに分類する。k平均法のアルゴリズムは次のようなステップからなる。
- 各クラスタ中心の初期値を設定する。
- 各データ点に対して、各クラスタ中心との距離を計算し、最も距離が近いクラスタを割り当てる。
- 各クラスタの平均ベクトル(重心)を計算する。
- 収束するまで、ステップ2、3の処理を繰り返す。
結果は、初期値のクラスタのランダムな割り振りに大きく依存することが知られており、1回の結果で最良のものが得られるとは限らない。そのため、何度か繰り返して行って最良の結果を選択する手法や、k-means++法のように初期値のクラスタ重心(セントロイド)同士の距離がなるべく遠くになるように改良した手法などが使用されることがある。
ハンズオン(k近傍法)
データを作成
# k近傍法
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 訓練データを作成
def gen_data():
x0 = np.random.normal(size=50).reshape(-1, 2) - 1
x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
x_train = np.concatenate([x0, x1])
y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
return x_train, y_train
X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
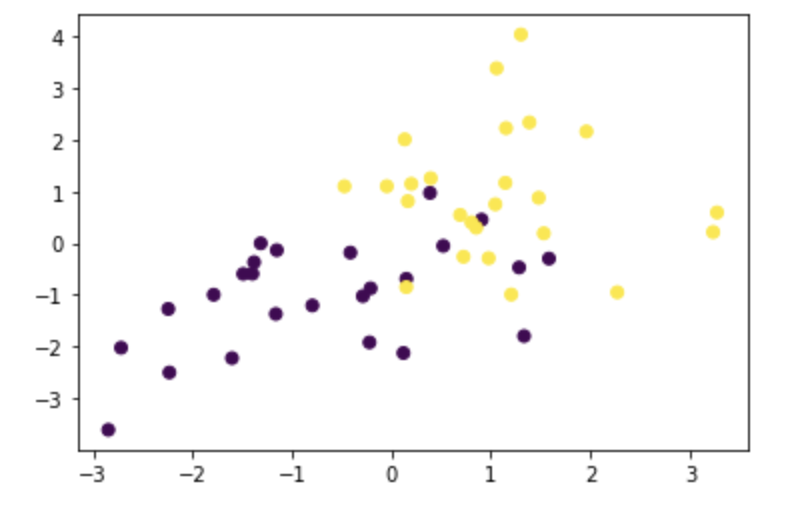
決定境界を描く
上記で与えられたデータの決定境界を決め、プロットする。
def distance(x1, x2):
return np.sum((x1 - x2)**2, axis=1)
def knc_predict(n_neighbors, x_train, y_train, X_test):
y_pred = np.empty(len(X_test), dtype=y_train.dtype)
for i, x in enumerate(X_test):
distances = distance(x, X_train)
nearest_index = distances.argsort()[:n_neighbors]
mode, _ = stats.mode(y_train[nearest_index])
y_pred[i] = mode
return y_pred
def plt_resut(x_train, y_train, y_pred):
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
plt.contourf(xx0, xx1, y_pred.reshape(100, 100).astype(dtype=np.float), alpha=0.2, levels=np.linspace(0, 1, 3))
k=3の時の決定境界をプロットする。
n_neighbors = 3
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
X_test = np.array([xx0, xx1]).reshape(2, -1).T
y_pred = knc_predict(n_neighbors, X_train, ys_train, X_test)
plt_resut(X_train, ys_train, y_pred)
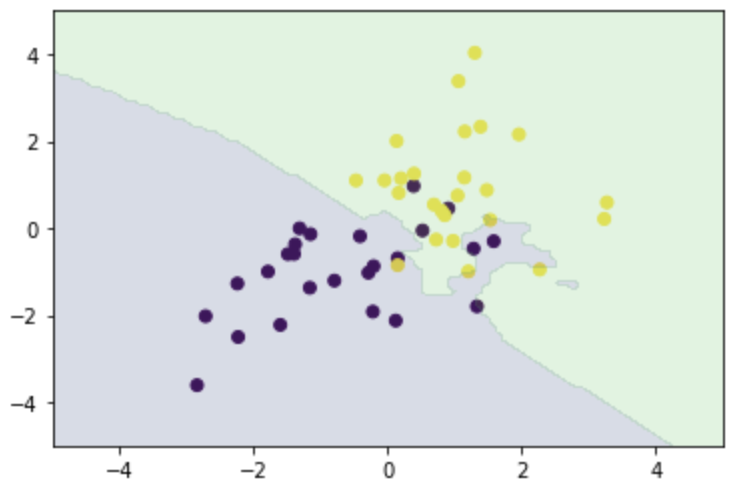
「n_neighbors = 3」を「n_neighbors = 8」とした時の決定境界をプロットしたものが以下の通り。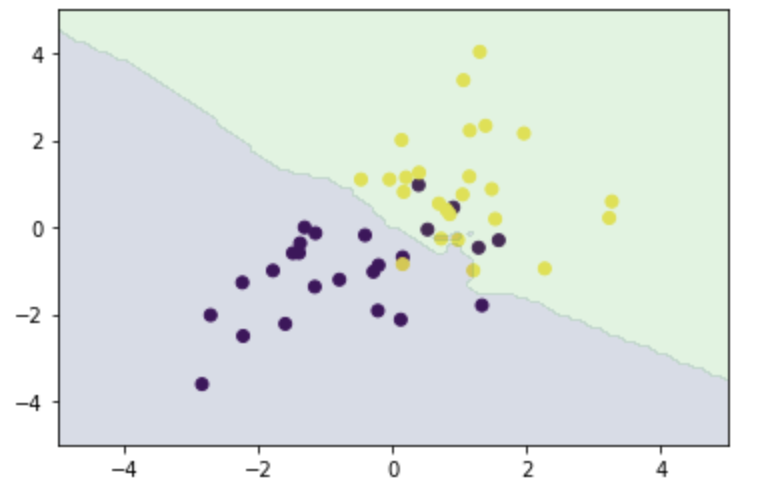
上記の2つのプロットを比べてみると、kが大きい方が、決定境界が滑らかになることが分かる。
サポートベクターマシーン
SVM(ハードマージン・ソフトマージン)
サポートベクターマシン(Support Vector Machine; SVM)は、教師あり学習であり、分類にも回帰にも使われるが、2値分類に使われることが多い。
2値分類においては、データ点$\boldsymbol{x}$を$y(x)=\boldsymbol{w}^T\phi(\boldsymbol{x})+b$の正負によって分類する。$\phi(\boldsymbol{x})$は特徴ベクトル。
境界$y(x)=\boldsymbol{w}^T\phi(\boldsymbol{x})+b=0$によって、各クラスのデータを分類する。各クラスのデータ点と境界との最短距離をマージンと呼ぶ。SVMでは、マージンが最大となる境界$y(x)=\boldsymbol{w}^T\phi(\boldsymbol{x})+b(=0)$におけるバラメータ$\boldsymbol{w},b$を学習する。この時、マージン上にある点をサポートベクトルと呼ぶ。
ソフトマージン(ある程度分類誤りを許容する)においては、マージン内に誤分類された時に正の値をとるスラック変数を導入して、次のように目的関数を表現する。 $$ 目的関数 \equiv C \sum_{i=1}^{n}\xi_i + \frac{1}{2}||\boldsymbol{w}||^2 \sim \frac{1}{2}\boldsymbol{w}^T \boldsymbol{w} + \sum_{i=1}^{n} \xi_i $$ 上式においては、次のようなことが言える。
- $C\to\infty$の時は、マージン内に訓練データが入ることや誤分類を一切許容しない。
- $C=\to0$の時は、誤分類が多くなる。
- 一般に過学習を防ぐためには、$C$を小さくする方がよい。
- $\xi_i=0$の時、ハードマージンSVMである。
- $\xi_i > 1$の時、超平面による分類に失敗している。
ハンズオン
ソフトマージンSVMのコードを試し、上記の$C$の値を変化させた時の振る舞いについて調べる。
テストデータは、次のように得る。それを可視化したグラフを以下に掲載する。
# サポートベクターマシン
# ソフトマージンSVMを試す
# テストデータの作成と描画
x0 = np.random.normal(size=50).reshape(-1, 2) - 1.
x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
x_train = np.concatenate([x0, x1])
y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
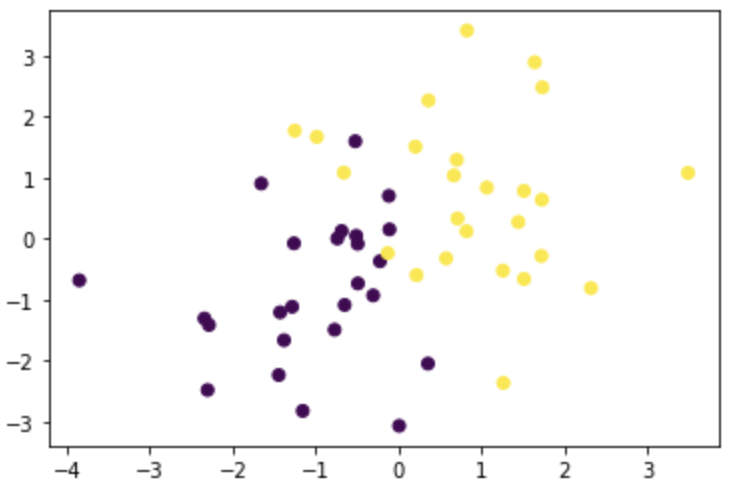
次に学習と予測のコードは次のとおり。
# 学習
X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)
n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)
C = 1
eta1 = 0.01
eta2 = 0.001
n_iter = 1000
H = np.outer(t, t) * K
a = np.ones(n_samples)
for _ in range(n_iter):
grad = 1 - H.dot(a)
a += eta1 * grad
a -= eta2 * a.dot(t) * t
a = np.clip(a, 0, C)
# 予測
index = a > 1e-8
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]
term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()
以下が可視化(描画)のコードと描画結果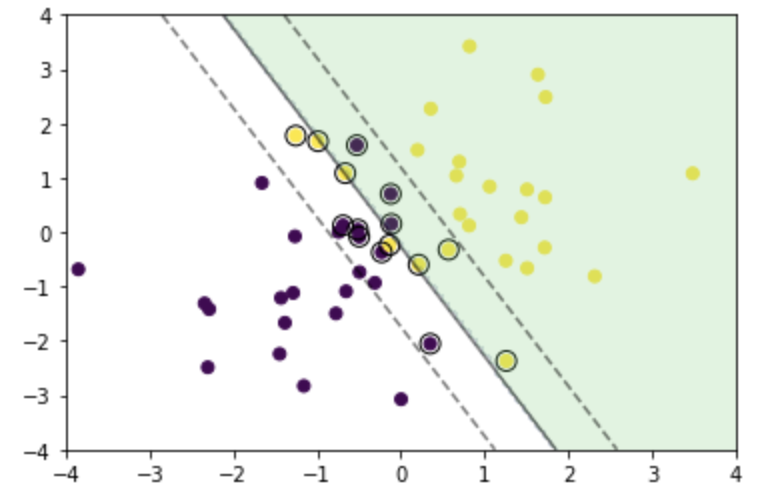
# 可視化準備と可視化(描画)
xx0, xx1 = np.meshgrid(np.linspace(-4, 4, 100), np.linspace(-4, 4, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)
# 訓練データを可視化
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
次に、学習時に「C = 1」とパラメータ設定した部分を、「C = 0.1」と「C = 10」とした場合の可視化結果を示す。
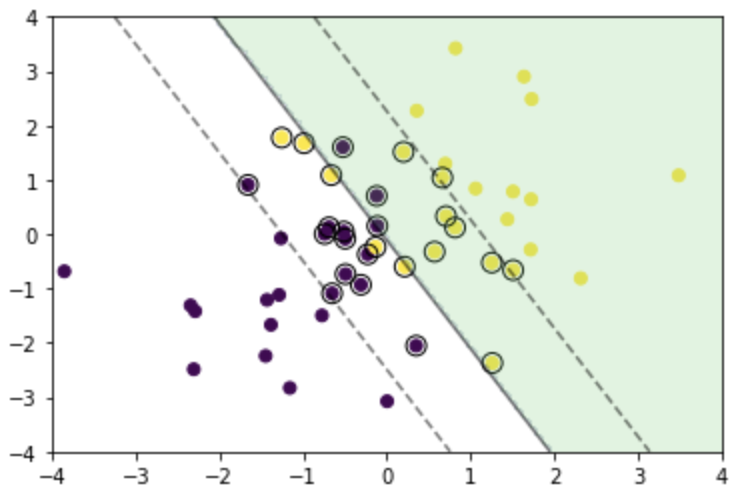
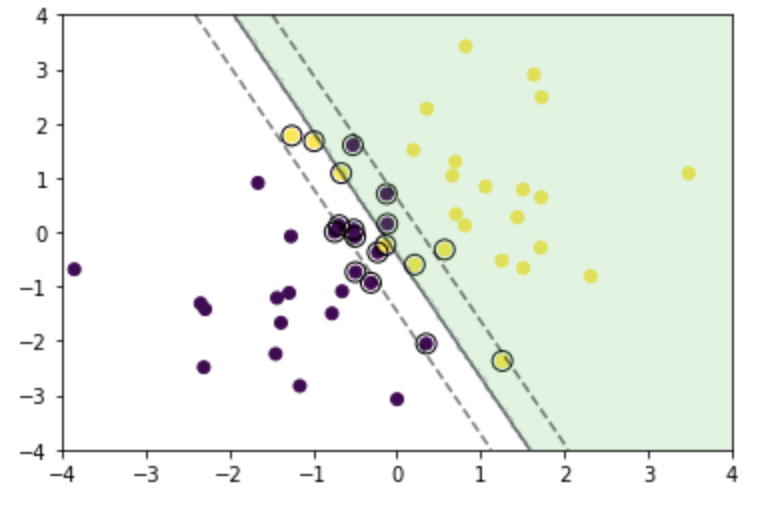
以上のように、Cを大きくすると、決定境界とマージンとの距離が小さくなり、誤分類を許さない方向にコントロールされることが分かる。