はじめに
この記事に引き続き、JDLA E資格のシラバスの範囲で、今回は「深層学習 day1およびday2」についてまとめたものである。「深層学習 day1およびday2」は、入力層、中間層、出力層、勾配降下法、誤差逆伝播などの深層学習の基本的な部分、および畳み込みニューラルネットワーク(Convolutional Neural Network; CNN)が範囲である。
参考文献
深層学習では、以下を参考としている。
- ゼロから作るDeep Learning 斎藤康毅著 オライリー・ジャパン
→ 実際にjupyter notebookでコードを試しながら学べる。数学的背景の説明は少ないが、最初に学ぶにはぴったりの一冊。誤差逆伝播法の「計算グラフ(computational graph)」の部分は分かりやすかった。Stage4のE資格受験資格認定テストの練習用にも、「E 5-2 誤差逆伝播法およびその他の微分アルゴリズム」でも同様の説明がある。 - 深層学習 Ian Goodfellow, Yoshua Bengio, AronCourville 著 岩澤有祐、鈴木雅大、中山浩太郎、松尾豊 監訳 ドワンゴ
→ Deep Learningの教科書的書籍。上記書籍で若干説明不足の数学的背景が追える。自分は、部分的にしか参照できていない。
深層学習day1
Section1:入力層〜中間層
概要
次のような入力層と中間層を構成するネットワーク(テキストのネットワーク図)において、$\boldsymbol{x}$が入力層に与えられた時、中間層の出力$z$は、次のようになる。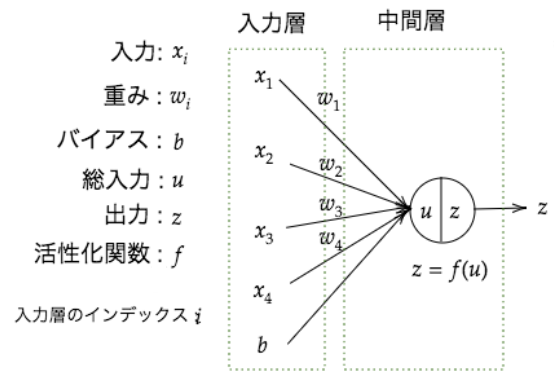 $$
\begin{align}
u &= w_1x_1+w_2x_2+w_3x_3+w_4x_4+b \\
&= \boldsymbol{W}\boldsymbol{x} + b \\
z &= f(u)
\end{align}
$$
ここで、$\boldsymbol{W} = (w_1, \cdots, w_i)^T, \boldsymbol{x}=(x_1,\cdots, x_i)^T$である。
$$
\begin{align}
u &= w_1x_1+w_2x_2+w_3x_3+w_4x_4+b \\
&= \boldsymbol{W}\boldsymbol{x} + b \\
z &= f(u)
\end{align}
$$
ここで、$\boldsymbol{W} = (w_1, \cdots, w_i)^T, \boldsymbol{x}=(x_1,\cdots, x_i)^T$である。
確認テスト
u1 =np.dot(x,W1)+b1について
内積部分の$np.dot(x,W1)$の$x$と$W1$は、上図($\boldsymbol{W}$と$\boldsymbol{x}$が1次元のベクトル)においては、入れ替えても成り立つが、次の理由により、この順序は重要である。
上図で中間層が3ノードと仮定すると、$\boldsymbol{W}$は4行3列の行列となる。この場合、$np.dot(x,W1)$と記述しなければ、内積計算は成り立たない。
実装演習
実装演習の結果、考察などについては、このページに記載した。
Section2:活性化関数
概要
活性化関数は、ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数のことである。この非線形の関数であることが重要である。
線形関数$h(x)=cx$を活性化関数とする。これを3層と層を重ねる(深くする)と、$y(x)=h(h(h(x)))$で表される。この計算結果は$y(x)=c\times c\times c\times x$、すなわち、$y(x)=c^3x=ax$となる。ここで$a=c^3$である。これでは、層を深くする意味がなくなってしまう。
活性化関数として、以下があげられる。
ステップ関数
$$ f(x) = \begin{cases} 1 & (x\ge 0) \\ 0 & (x < 0) \end{cases} $$
シグモイド関数
$$ f(x) = \frac{1}{1 + \exp(-x)} $$
ReLU関数
$$ f(x) = \begin{cases} x & (x\ge 0) \\ 0 & (x < 0) \end{cases} $$
実装演習
実装演習の結果、考察などについては、こちらのページに記載した。
Section3:出力層
概要
ニューラルネットワークは、回帰問題と分類問題の何にも用いることができる。回帰問題、分類問題のどちらに対応させるかにより、出力層の活性化関数を変更する必要がある。一般的に、回帰問題では恒等関数を、分類問題ではソフトマックス関数を使う。
誤差関数(損失関数;loss function)
誤差関数は、予想データと正解データの出力の間にどのくらいの誤差があるのかを評価する関数である。誤差関数は、扱う問題によって次のように使い分けられる。
- 回帰問題:平均二乗誤差(MSE)関数
- 分類問題:クロスエントロピー誤差
平均二乗誤差
平均二乗誤差は、次の式で表される。 $$ E_n(w) = \frac{1}{2}\sum_{i=1}^N (y_i - d_i)^2 = \frac{1}{2}||(y-d)||^2 $$ ここで、$y_i$はニューラルネットワークの出力、$d_i$は教師データを表し、$N$はデータの次元数である。
この平均二乗誤差で、2乗することにより全て正の値の凸関数となる。$\frac{1}{2}$は誤差関数を微分した際、式を簡潔にするためである。
クロスエントロピー誤差
クロスエントロピー誤差は、次の式で表される。 $$ E_n(w) = - \sum_{i=1}^N d_i \log y_i $$ ここで、$y_i$はニューラルネットワークの出力、$d_i$は教師データを表し、$N$はデータの次元数である。
確認テスト
ソフトマックス関数
次のソフトマックス関数を実装したソースコードで処理を説明する。 $$ f(i,u) = \frac{\exp(u_i)}{\sum_{k=1}^K \exp(u_k)} $$
# 出力層の活性化関数
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
If x.ndim == 2:のブロックは、ミニバッチに対応するための処理。本質的には、return行のnp.exp(x)/np.sum(np.exp(x)がソフトマックス関数の式を処理している。
その直前のx = x - np.max(x)は、オーバーフロー対策のため。その根拠は、次の式の通りである。 $$ \frac{\exp(a_k)}{\sum_{i=1}^n \exp(a_i)} = \frac{C\exp(a_k)}{C\sum_{i=1}^n\exp(a_i)}=\frac{\exp(a_k+\log C)}{\sum_{i=1}^n\exp(a_i+\log C)}=\frac{\exp(a_k+C’)}{\sum_{i=1}^n\exp(a_i+C’)} $$ ここで、$C,C’$は共に任意の実数。変形中には$a^{log_a b}=b$であるを利用している。
交差エントロピー
次の交差エントロピーを実装したソースコードを説明する。 $$ E_n(w) = - \sum_{i=1}^N d_i \log y_i $$
# クロスエントロピー
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
上のコードで、if y.ndim == 1:で、1次元の場合の処理を行う。次のif d.size == y.size:では、one-hot-vectorの場合に、1が立っているインデックスを求めている。交差エントロピーの本質的な処理部分は、最後のreturn文の-np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) である。1e-7は、$\log 0$が$-\infty$になることを防ぐため、小さな値を加えることで、ゲタをはかして(嵩上げして)いる。
Section4:勾配降下法
概要
勾配降下法(Gradient descent)
勾配降下法は、誤差関数$E(w)$を最小化するパラメータ$w$を発見する手法であり、次の式により求める。 $$ \boldsymbol{w^{(t+1)}} = \boldsymbol{w^{(t)}} - \epsilon\nabla E $$ ここで、$\epsilon$は学習率である。学習率$\epsilon$はハイパーパラメータの一つであり、学習率$\epsilon$の値により学習の効率が大きく異なる。
学習率$\epsilon$が小さい場合、発散することはないが、小さすぎると収束するまでに時間がかかる。学習率$\epsilon$が大き過ぎると極小値にたどり着かず発散する可能性がある。勾配降下法のアルゴリズムには次のようなものがある。
- Momentum
- AdaGrad
- Adam
確率的勾配降下法(Stochastic Gradient descent; SGD)
確率的勾配降下法は、ランダムに抽出したサンプル誤差を用いて、パラメータを更新する手法であり、次の式により求める。 $$ \boldsymbol{w^{(t+1)}} = \boldsymbol{w^{(t)}} - \epsilon\nabla E_n $$ 勾配降下法に比べて、次のようなメリットがある。
- データが冗長な場合の計算コストが削減できる。
- 望まない局所極小解に収束するリスクが軽減するする。
- (データが逐次増加するような)オンライン学習に対応できる。
ミニバッチ勾配降下法
ミニバッチ勾配降下法は、ランダムに分割したデータの集合(ミニバッチ)$D_t$に属するサンプルの平均誤差により、パラメータを更新する手法であり、次の式により求める。 $$ \begin{align} \boldsymbol{w^{(t+1)}} &= \boldsymbol{w^{(t)}} - \epsilon\nabla E_t \\ E_t &= \frac{1}{N_t}\sum_{n\in D_t} E_n \\ N_t &= |D_t| \end{align} $$ ミニバッチ勾配降下法は、確率的勾配降下法のメリットを損わず、並列処理することができ、計算資源を有効利用ができる。CPUでのスレッドやGPUのSMを使った並列化が可能な手法である。
確認テスト
勾配降下法の意味を図示
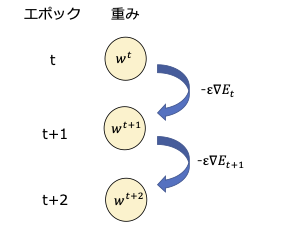
次の式の意味を図示する。
$$
\boldsymbol{w^{(t+1)}} = \boldsymbol{w^{(t)}} - \epsilon\nabla E_t
$$
Section5:誤差逆伝播法(Backpropagation)
概要
誤差逆伝播法は、算出された誤差を、出力層から順に微分し、前の層へと伝播させることで、最小限の計算で各パラメータでの微分値を解析的に計算する手法である。
計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。
確認テスト
誤差逆伝播法で、既に行った計算結果を保持しているコードを抽出
以下は、確率的勾配降下法の節で使った誤差逆伝播関数のコードである。
# 誤差逆伝播
def backward(x, d, z1, y):
# print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = functions.d_mean_squared_error(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
#delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
## 試してみよう
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
delta1 = delta1[np.newaxis, :]
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
# print_vec("偏微分_重み1", grad["W1"])
# print_vec("偏微分_重み2", grad["W2"])
# print_vec("偏微分_バイアス1", grad["b1"])
# print_vec("偏微分_バイアス2", grad["b2"])
return grad
上のコードで、出力層において、順伝播による予測値と教師データとから微分結果がdelta2である。このdelta2は、前の層(中間層)の微分結果delta1を求める時に使われている。
実装演習
実装演習の結果、考察などについては、こちらのページに記載している。
深層学習day2
Section1:勾配消失問題
概要
勾配損失問題とは
誤差逆伝播法では、確率的勾配降下法を用いて、誤差の最小化を求める。すなわち、誤差を出力層から入力層に向かって逆向きに伝播しながら勾配を計算し、隠れ層の重みやバイアスが再計算する。
誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。これを勾配損失問題という。
勾配損失問題が発生する仕組み
活性化関数がシグモイド関数とすると、シグモイド関数の値の範囲は、このグラフのように0から1を緩やかに変化する。値が大きくなっても、出力の変化が微小なため、勾配損失問題を引き起こすことになる。
解決方法
- 活性化関数の選択:ReLU関数などを使用する。
- 重みの初期値設定:XavierやHeを使って重みを初期化する。
- バッチ正則化:ミニバッチ単位で、入力値のデータの偏りを抑制する。
確認テスト
連鎖律を用いてdz/dxを求める(10ページ)
$$ \begin{align} z &= t^2 \\ t &= x + y \end{align} $$
上記の時に、連鎖律を用いて、$\frac{dz}{dx}$を求める。 $$ \frac{dz}{dx} = \frac{dz}{dt}\frac{dt}{dx} = 2t \times 1=2(x+y) $$
シグモイド関数を微分した時、入力値が0の時に最大値を取る、その値は?(18ページ)
シグモイド関数、およびその微分は、次の通り。 $$ \begin{align} f(x) &= \frac{1}{1+\exp(-x)} \\ f’(x) &= (1-f(x))f(x) \end{align} $$ したがって、$f’(0)=(1-f(0))f(0)=0.25$となる。$f(0)=0.5$であることより。
バッチ正則化の効果
バッチ正規化を行うメリットは、次の通りである。
- 中間層の重みの更新が安定化し、結果として、学習がスピードアップする。
- 過学習を抑えることができる。
実装演習
実装演習の結果、考察などについては、このページに記載している。
Section2:学習率最適化手法
概要
学習率
学習率は、Day1の「Section4:勾配降下法」で触れたように、次のように学習効果に影響を及ぼす。
- 学習率の値が大きい場合
- 最適値にいつまでもたどり着かず発散してしまう。
- 学習率の値が小さい場合
- 発散することはないが、小さすぎると収束するまでに時間がかかってします。
- 大域局所最適値に収束しずらくなる。
初期の学習率設定については、次のように考える。
- 初期の学習率を大きく設定し、徐々に学習率を小さくしていく。
- パラメータ毎に学習率を可変させる。
学習率最適化手法
以下、各学習率最適化手法についてまとめる。
モメンタム
誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算する。次の式で与えられる。$\mu$は慣性である。 $$ \begin{align} V_t &= \mu V _{t-1} - \epsilon \nabla E \\ \boldsymbol{w^{(t+1)}} &= \boldsymbol{w^{(t)}} + V_t \end{align} $$ 次のようなメリットがある。
- 局所的最適解にはならず、大域的最適解となる。
- 谷間についてから最も低い位置(最適値)に行くまでの時間が早い。
AdaGrad
誤差をパラメータで微分したものと再定義した学習率の積を減算する。次の式で与えられる。 $$ \begin{align} h_0 &= \theta \\ h_t &= h_{t-1} + (\nabla E)^2 \\ \boldsymbol{w^{(t+1)}} &= \boldsymbol{w^{(t)}} - \epsilon \frac{1}{\sqrt{h_t}+ \theta}\nabla E \end{align} $$ AdaGradのメリットは次の通り。
- 勾配の緩やかな斜面に対して、最適値に近づける。
一方次のような課題もある。
- 学習率が徐々に小さくなるので、鞍点問題を引き起こす事があった。
RMSProp
誤差をパラメータで微分したものと再定義した学習率の積を減算する。次の式で与えられる。 $$ \begin{align} h_t &= \alpha h_{t-1} + (1-\alpha)(\nabla E)^2 \\ \boldsymbol{w^{(t+1)}} &= \boldsymbol{w^{(t)}} - \epsilon \frac{1}{\sqrt{h_t}+ \theta}\nabla E \end{align} $$ RMSPropのメリットは次の通り。
- 局所的最適解にはならず、大域的な最適解となる。
- ハイパーパラメータの調整が必要な場合が少ない。
Adam
Adamは、モメンタムおよびRMSPropのメリットを含んだアルゴリズムである。具体的には次の通り。
- モメンタムの過去の勾配の指数関数的減衰平均。
- RMSPropの過去の勾配の2乗の指数関数的減衰平均。
確認テスト
モメンタム・AdaGrad・RMSPropの特徴を説明(44ページ)
前節の学習立最適化手法でまとめた通り。
実装演習
実装演習の結果、考察などについては、このページに記載している。
Section3:過学習
概要
過学習
過学習とは、テスト誤差と訓練誤差とで学習曲線が乖離すること。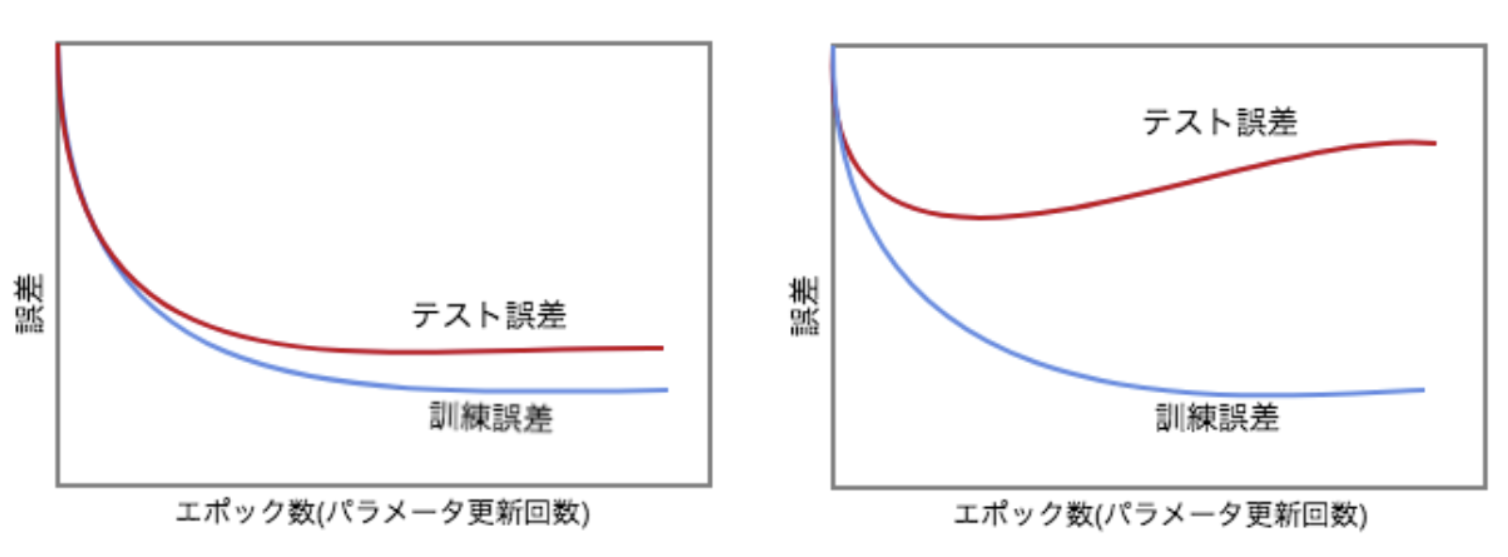
原因としては次の通り。
- パラメータの数が多い。
- パラメータの値が適切でない。
- ノードが多い。
つまり、ネットワークの自由度(回数、ノード数、パラメータの値、等)が高すぎるということである。
正則化
正則化とは、ネットワークの自由度(回数、ノード数、パラメータの値、等)を制約すること。
正規化手法を利用して過学習を抑制する。正則化手法には、次のような手法がある。
- L1正則化、L 2正則化
- ドロップアウト
Weight decay(荷重減衰)
過学習の原因として、重みが大きい値を取ることで、過学習が発生することがある。
過学習の解決策として、誤差に対して、正則化公を加算することで、重みを抑制する。
確認テスト
リッジ回帰の特徴は?(59ページ)
- ハイパーパラメータを大きな値に設定すると、全ての重みが限りなく0に近づく。
- ハイパーパラメータを0に設定すると、非線形回帰となる。
- バイアス項についても、正則化される。
- リッジ回帰の場合、隠れ層に対して正則化項を加える。
→ 正しいのは、項番3。
実装演習
実装演習の結果、考察などについては、こちらの記事にまとめた。
Section4:畳み込みニューラルネットワークの概念
概要
畳み込みニューラルネットワーク(Convolutional Neural Network; CNN)は、画像認識や音声認識など幅広い分野で使われているニューラルネットワークである。
2012年ILSVRC(ImageNet Large Scale Visual Recognition Challenge)においてCNNを利用した「AlexNet」がそれまでの手法に大差をつけて優勝した。それ以降、ILSVRCではCNNを利用した手法が主流となり、毎年新たなCNNモデルが考案され精度の向上に寄与し続けている。このように、CNNは画像認識分野を中心に大いに注目されている。
参考文献
AlexNetの論文についてはこちらページを参照。この論文は被引用数5万を超える非常に有名な論文である。
ネットワーク構成
これまで学び・実装した全結合(fully- connected)層のみで構成されたネットワークに対し、CNNでは畳み込み層(Convolution layer)、プーリング層(pooling layer)が追加されたネットワーク構成である。
畳み込み層
畳み込み層の特徴は、3次元の空間情報も学習できるような層である。画像データの場合、縦・横・チャンネルの3次元データを受け取り、同じく3次元データとして、次の層に出力するので、CNNでは、画像などの形状を有したデータを正しく理解できる。
畳み込み層で行う処理は、畳み込み演算である。畳み込み演算は、画像処理でのフィルタ演算に相当する。即ち、入力データにフィルタを作用させ、出力データを得る。
畳み込み演算で登場する処理が、パディング(入力データの周囲の仮想的なデータ処理)とストライド(フィルターの移動間隔)である。
入力画像サイズ(IH、IW)、フィルタサイズ(FH、FW)、ストライドをS、パディングをP、とした時の出力画像サイズ(OH、OW)は、次の式で与えられる。 $$ OH = \frac{IH+2\times P-FH}{S}+1, \qquad OW= \frac{IW+2\times P-FW}{S}+1 $$
プーリング層
プーリングは、縦・横方向の空間を小さくする演算である。「2 × 2のMaxプーリング」は、入力データの2×2領域ごとの最大値を出力データとする処理である。この時もストライドにより移動量を指定する。
プーリング層には、次の特徴がある。
- 学習するパラメータがない:プーリングは、対象領域から最大値を取る(もしくは平均を取る)だけの処理であり、学習すべきパラメータは存在しない。
- チャネル数は変化しない:プーリングの演算はチャンネルごとに独立して計算され、入出力でチャンネル数は変化しない。
確認テスト
畳み込み処理での出力サイズ(95ページ)
入力サイズ6×6、フィルタサイズ2×2、ストライドとパディングを1の場合、畳み込み結果の出力サイズ?
幅について、以下の式で出力サイズが求められる。ここで$P$はパディングサイズ。 $$ OH = \frac{IH+2\times P - F H }{S} + 1= \frac {6 + 2\times 1 - 2}{1}+1 = 7 $$ 同様に幅も求めて、出力サイズとして、7×7を得る。
実装演習
実装演習の結果、考察などについては、こちらの記事にまとめた。
Section5:最新のCNN
概要
本節は、「最新のCNN」とのタイトルではあるが、2012年のAlexNetに関するものである。最新は複雑になりすぎているので、この世界では古典的なAlexNetについて学んだようが初学者には理解しやすいとのこと。
AlexNetの構成
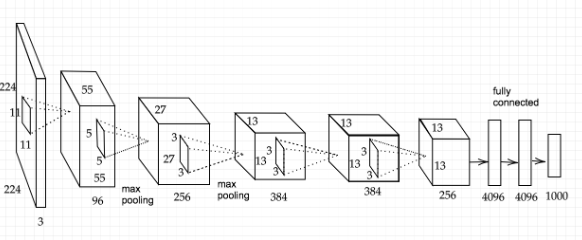
入力層は、224×224の3チャンネルカラー画像。
出力層は、(ISLVRC 2012において1000クラスの画像を識別するため)softmax関数で確率を示す1000次元のベクトル(各次元の出力確率)。
畳み込み層が5層(Conv1-5)、プーリング層が3層(P1-3)(畳み込み層の1層目Conv1、 2層目Conv 2、5層目Conv5の直後)、全結合層(F C6-7)が3層から成る。
活性化関数にはReLUが使われている。
AlexNetの特徴
ReLUの導入
従来のニューラルネットワークでは、シグモイド関数やtanh関数が用いられていたが、勾配損失の回避、学習の高速化のため、ReLU関数が用いられている。
過学習の削減
パラメータ数が多いAlexNetにおいては、過学習をいかに抑えるかが非常にポイントであった。そのために、いくつかの過学習抑制のための手法が使われている。
ここでは、Dropoutによる正則化について説明する。
ネットワーク終盤の全結合層2つ(FC6、FC7)のニューロンに対し、ドロップ確率0.5でドロップアウトし、過学習を大幅に削減している。
GPUを使用
畳み込み層をチャンネル方向に 2分割し、2つのGPUに処理を分散させ、並列処理を実施している。今日では、深層学習ではGPUが当然のように用いられており、その先鞭である。
まとめ
AlexNetは、大規模モデルの画像認識をCNNで実現できることを示した意味で歴史的である。そこには過学習をいかに抑制するかが非常に重要であった。
AlexNetはCNNの層をシンプルに積み上げることで、画像認識精度を高めたものであったが、その後、先端の研究者がさまざまなモデルに取り組み、GoogLenet、ReSNetなどに発展していく。
以上にように、AlexNetは、大規模なCNNで実現する上での多くの貢献を残した。
確認テスト
畳み込み処理での出力サイズ(day3 テキストの最初の部分にあり)
入力サイズ5×5、フィルタサイズ3×3、ストライド2とパディング1での、畳み込み結果の出力サイズ?
幅について、以下の式で出力サイズが求められる。ここで$P$はパディングサイズ。 $$ OH = \frac{IH+2\times P - F H }{S} + 1= \frac {5 + 2\times 1 - 3}{2} + 1 = 3 $$ 同様に幅も求めて、出力サイズとして、3×3を得る。
実装演習
実装演習の結果、考察などについては、こちらの記事にまとめた。