はじめに
深層学習day2の「Section3:過学習」の実装演習を以下にまとめる。
実装演習
「2_5_overfiting.ipynb」のコードを参照した。
weight decay L2
正則化強度パラメータ「weight_decay_lambda」の値を0.08, 0.1, 0.15, 0.2と変化させて、結果がどう変わるかを試した。
コードは、以下の通り。
# 自分の環境で、ダウンロードした共通関数の格納フォルダのパス
import sys
sys.path.append('DNN_code_colab_lesson_1_2')
sys.path.append('DNN_code_colab_lesson_1_2/lesson_2')
import numpy as np
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from multi_layer_net import MultiLayerNet
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.1
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy - WDL=0.1")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
グラフ表示の結果は、次の通り。
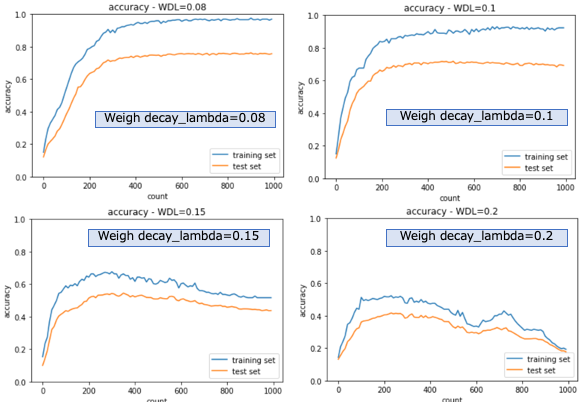
$0.08〜0.2$の少しの変化で、学習結果(正解率)に大きな変化が出ることがわかった。
正則化強度パラメータ(weight_decay_lambda)がある値(この例では、0.1と0.15の間)以上になると、学習結果が低下し、更に正則化強度パラメータを上げていくと(これ例では、0.15と0. 2の間)、学習を進めても下がり始める現象も見られた。