(その2)の記事の続き。
前回は、VGG16で学習をしたが、今回はモデルにResNetを使ってみる。
VGG、ResNetと言えば、ちょうど一年前にE資格の勉強で学んだ記憶が蘇る。
VGG (Simonyan & Zisserman, 2014)は、2014年に提案されたモデルで、フィルタサイズ$3\times3$の畳み込み層を複数積み重ねることで、少ないパラメータで大きなフィルタを使用した場合と同じ範囲を畳み込むことができるモデルである。 ResNet (He et al., 2015)は、2015年に提案された特徴マップ同士を足し合わせるショートカット結合が特徴的なモデルである。
訓練用とテスト用のDataLoaderを作成するところまでは、VGG16と共通。
ResNetモデル
残差ブロック部分は次の通り。
import torch
import torch.nn as nn
class block(nn.Module):
def __init__(self, first_conv_in_channels, first_conv_out_channels, identity_conv=None, stride=1):
"""
残差ブロックを作成するクラス
Args:
first_conv_in_channels : 1番目のconv層(1×1)のinput channel数
first_conv_out_channels : 1番目のconv層(1×1)のoutput channel数
identity_conv : channel数調整用のconv層
stride : 3×3conv層におけるstide数。sizeを半分にしたいときは2に設定
"""
super(block, self).__init__()
# 1番目のconv層(1×1)
self.conv1 = nn.Conv2d(
first_conv_in_channels, first_conv_out_channels, kernel_size=1, stride=1, padding=0)
self.bn1 = nn.BatchNorm2d(first_conv_out_channels)
# 2番目のconv層(3×3)
# パターン3の時はsizeを変更できるようにstrideは可変
self.conv2 = nn.Conv2d(
first_conv_out_channels, first_conv_out_channels, kernel_size=3, stride=stride, padding=1)
self.bn2 = nn.BatchNorm2d(first_conv_out_channels)
# 3番目のconv層(1×1)
# output channelはinput channelの4倍になる
self.conv3 = nn.Conv2d(
first_conv_out_channels, first_conv_out_channels*4, kernel_size=1, stride=1, padding=0)
self.bn3 = nn.BatchNorm2d(first_conv_out_channels*4)
self.relu = nn.ReLU()
# identityのchannel数の調整が必要な場合はconv層(1×1)を用意、不要な場合はNone
self.identity_conv = identity_conv
def forward(self, x):
identity = x.clone() # 入力を保持する
x = self.conv1(x) # 1×1の畳み込み
x = self.bn1(x)
x = self.relu(x)
x = self.conv2(x) # 3×3の畳み込み(パターン3の時はstrideが2になるため、ここでsizeが半分になる)
x = self.bn2(x)
x = self.relu(x)
x = self.conv3(x) # 1×1の畳み込み
x = self.bn3(x)
# 必要な場合はconv層(1×1)を通してidentityのchannel数の調整してから足す
if self.identity_conv is not None:
identity = self.identity_conv(identity)
x += identity
x = self.relu(x)
return x
次にResNet本体の部分。conv2, conv3, conv4, conv5は、残差ブロックで構成される。
class ResNet(nn.Module):
def __init__(self, block, num_classes):
super(ResNet, self).__init__()
# conv1はアーキテクチャ通りにベタ打ち
self.conv1 = nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3)
self.bn1 = nn.BatchNorm2d(64)
self.relu = nn.ReLU()
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
# conv2_xはサイズの変更は不要のため、strideは1
self.conv2_x = self._make_layer(block, 3, res_block_in_channels=64, first_conv_out_channels=64, stride=1)
# conv3_x以降はサイズの変更をする必要があるため、strideは2
self.conv3_x = self._make_layer(block, 4, res_block_in_channels=256, first_conv_out_channels=128, stride=2)
self.conv4_x = self._make_layer(block, 6, res_block_in_channels=512, first_conv_out_channels=256, stride=2)
self.conv5_x = self._make_layer(block, 3, res_block_in_channels=1024, first_conv_out_channels=512, stride=2)
self.avgpool = nn.AdaptiveAvgPool2d((1,1))
self.fc = nn.Linear(512*4, num_classes)
def forward(self,x):
x = self.conv1(x) # in:(3,224*224)、out:(64,112*112)
x = self.bn1(x) # in:(64,112*112)、out:(64,112*112)
x = self.relu(x) # in:(64,112*112)、out:(64,112*112)
x = self.maxpool(x) # in:(64,112*112)、out:(64,56*56)
x = self.conv2_x(x) # in:(64,56*56) 、out:(256,56*56)
x = self.conv3_x(x) # in:(256,56*56) 、out:(512,28*28)
x = self.conv4_x(x) # in:(512,28*28) 、out:(1024,14*14)
x = self.conv5_x(x) # in:(1024,14*14)、out:(2048,7*7)
x = self.avgpool(x)
x = x.reshape(x.shape[0], -1)
x = self.fc(x)
return x
def _make_layer(self, block, num_res_blocks, res_block_in_channels, first_conv_out_channels, stride):
layers = []
# 1つ目の残差ブロックではchannel調整、及びsize調整が発生する
# identifyを足す前に1×1のconv層を追加し、サイズ調整が必要な場合はstrideを2に設定
identity_conv = nn.Conv2d(res_block_in_channels, first_conv_out_channels*4, kernel_size=1,stride=stride)
layers.append(block(res_block_in_channels, first_conv_out_channels, identity_conv, stride))
# 2つ目以降のinput_channel数は1つ目のoutput_channelの4倍
in_channels = first_conv_out_channels*4
# channel調整、size調整は発生しないため、identity_convはNone、strideは1
for i in range(num_res_blocks - 1):
layers.append(block(in_channels, first_conv_out_channels, identity_conv=None, stride=1))
return nn.Sequential(*layers)
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = ResNet(block, 10).to(device)
ResNetのインスタンスを作成した後は、VGG16の「訓練と評価関数群」、「実行部分」、「グラフ化」のcellと共通である。
結果
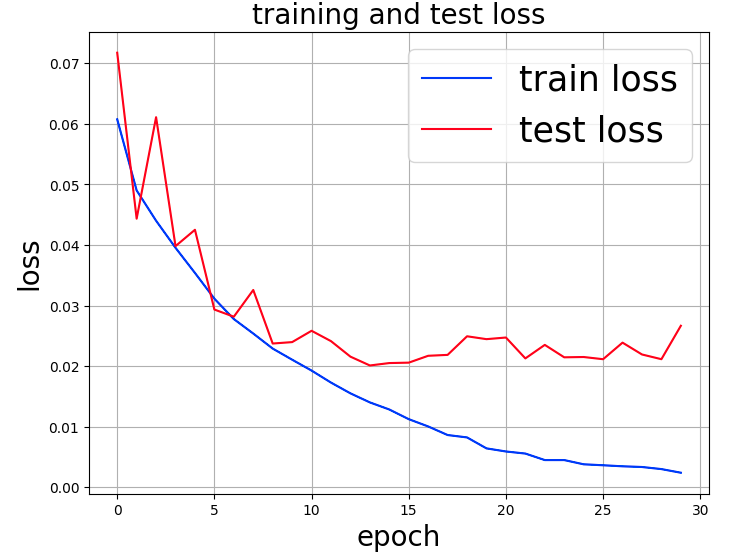
VGG16と比較するとエポックが進むと誤差が減少するも、8エポックあたりから過学習の傾向を示している。
30エポックに掛かった時間は、2,391秒(39分51秒)とVGG16の86%であった。
次にVGG16の時と同じように、銀河イメージに回転や左右反転をtransformsで指定した結果は次の通り。
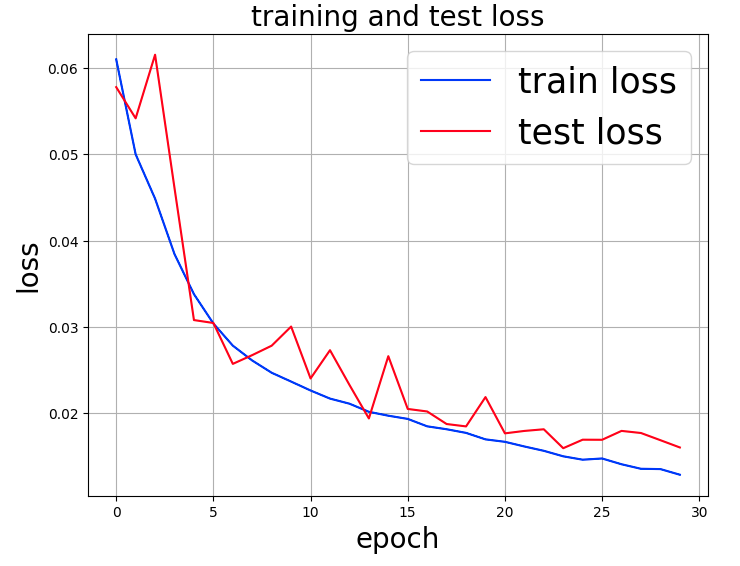
30回のエポックまで、過学習の傾向もなく、誤差が減少していることが分かる。この時の所要時間は、2,508秒(41分48秒)であった。
まとめ
今回の銀河の形状分類においては、誤差の収束、所要時間の観点で、ResNetの方がVGG16より良い結果となった。VGG16を使う場合は、学習率$lr$を適切に設定する必要がある。
画像処理で畳み込みを使わずに、最先端レベル(State-of-The-Art; SoTA)と言われている、Transformerを用いたVision Transformer(ViT)による分類を試してみたい。