PINNs 〜 質点・バネ・ダンパー問題

 December 19, 2024に投稿  |  Kenji Arai  • 翻訳：en

モチベーション

一年以上も前に、NVIDIA Modulusを使って、PINNs（Physics-Informed Neural Networks）を試したが、その後全く手付かずだった。最近のセミナーで理研・松岡さんの講演（AI for Science; こちらとかこちらのイベントでの講演）を聴講して、改めて勉強してみようと思い、物理的にも理解し易い問題を例にして、PINNsの実装に挑戦した。

情報源

  1. PINNs(Physics Informed Neural Networks)に挑戦してみた - 実装面で参考にしたページ。コードは写経せずに、コードの内容を理解した上で自分の手でコーディングした。
  2. KIT物理ナビゲーション - 質点・バネ・ダンパーモデル（減衰振動）の微分方程式の理解に参考にした。二次方程式の解、オイラーの公式、三角関数の加法定理なども思い出しながら、手を動かして、微分方程式を解く道筋を理解した。
  3. PytorchでPINNs(Physics Informed Neural Network)を実装してみる - 同じ問題（質点・バネ・ダンパーモデル）を実装しているページ。

物理的背景

コードの見通しを良くするため、背景となる考え方を以下にまとめる。

微分方程式

質点・バネ・ダンパーモデルを表す微分方程式は次の通り。 $$ m\frac{d^2x}{dt^2}+c\frac{dx}{dt}+kx=0 \tag{1} $$ $m$は質量（mass）、$c$は減衰係数（damping coefficent）、$k$はバネ定数（spring constant）である。

ここで、$\gamma=\frac{c}{2m}$、$\omega_0=\sqrt{\frac{k}{m}}$とすると、(1)式は次の通り。 $$ \frac{d^2x}{dt^2} + 2\gamma\frac{dx}{dt}+\omega_0^2x=0 \tag{2} $$ (2)式を解くと（情報源2.を参考のこと）次の通りとなる。 $$ x= \exp^{-\gamma t}(A_1\cos \omega t+A_2 \sin\omega t) \tag{3} $$ ここで、$\omega=\sqrt{\omega_0^2 - \gamma^2}$とし、境界条件として、$t=0$の時の位置を$x_0$、速度を$v_0$とする。更に、$A_1= x_0$、$A_2=\frac{x_0\gamma+v_0}{\omega}$とする。

有限差分法向け

(1)式より、ある時点の加速度を$a_i$とすると、次のように表せる。 $$ a_i=-\frac{c v_i+k x_i}{m} \tag{4} $$ 速度と変位は次の通り。 $$ x_{i+1} = x_i + \frac{dx}{dt}\Delta t \tag{5} $$

$$ v_{i+1} = v_i + \frac{dv}{dt}\Delta t \tag{6} $$

損失関数の考え方

観測データ（今回は、厳密解から5つを選んだ）との誤差を表す損失関数は次の通り。 $$ L_{obs} = \frac{1}{M}\sum_{i}^{m} (M_{pinn}(t_i)-O(t_i))^2 \tag{7} $$ ここで、$M_{pinn}(t_i)$はモデルを使った推論結果、$O(t_i)$は観測データであり、$M$は観測データ数。(7)式は通常のモデルの学習時の平均二乗誤差（MSE）と同じである。

次に、物理誤差（微分方程式との誤差）を表す損失関数は次の通り。 $$ L_{pinn} = \frac{1}{N}\sum_{j}^{n}(f(t_j))^2 \tag{8} $$ ここで、$f(t_j)$は、物理現象を表す微分方程式であり、$N$はある時間区分の刻み数。(8)式は微分方程式(1)を成立する方向に働く。

今回の場合の損失関数は、(7)と(8)を合わせてもので表現する。 $$ L_{total} = L_{obs} + \lambda_1 L_{pinn} \tag{9} $$ ここで、$\lambda_{1}$は、観測データの誤差と微分方程式からの誤差の重み付けのパラメータである。

コードと結果

有限差分法

# Finite Diffrence Method
import numpy as np

def FiniteDiff(m, c, k, x0, v0, ts):
    """
    Input:
    m: mass [Kg]
    c: damping coefficent [N.s/m]
    k: spring constant [N/m]
    x0: initial position [m]
    v0: initial velocity [m/s]
    ts: list of time step [s]

    Output:
    x: list of potision at each time step [m]
    """
    x = np.zeros_like(ts)
    v = np.zeros_like(ts)
    
    x[0] = x0
    v[0] = v0
    dt = ts[1] - ts[0]
    
    for i in range(len(ts)-1):
        a = -(c*v[i] + k*x[i])/m
        v[i+1] = v[i] + a*dt
        x[i+1] = x[i] + v[i+1]*dt

    return x

厳密解

# Analytical Solution

def AnalyticalSol(m, c, k, x0, v0, ts):
    g = c/(2*m)  # gamma
    w0 = np.sqrt(k/m)  # omega 0
    w = np.sqrt(w0*w0 - g*g)
    A1 = x0
    A2 = (x0*g + v0)/w
    x = np.exp(-g*ts) * (A1*np.cos(w*ts) + A2*np.sin(w*ts))
    
    return x

初期値

# Initial values

m = 1.0
c = 0.4
k = 10.0
x0 = 1.0
v0 = 0.0
elasped_t = 10.0
n_step = 1000

ts = np.linspace(0, elasped_t, n_step)

FDMと厳密解を求め、グラフ化

# Solve the problem using Finite Difference Method and analytical solution

x_fd = FiniteDiff(m, c, k, x0, v0, ts)
x_as = AnalyticalSol(m, c, k, x0, v0, ts)

# Draw graphs of time-specific deviations from FDM and Analytical Solution

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(12,8))

ax1 = fig.add_subplot(2, 1, 1)
ax1.plot(ts, x_fd, c='b', label='FiniteDiff')
ax1.set_xlabel('time step', fontsize='14')
ax1.set_ylabel('deviations', fontsize='14')
ax1.set_title('FDM: time-specific deviations', fontsize='18')
ax1.grid()
ax1.legend(fontsize='14')

ax2 = fig.add_subplot(2, 1, 2)
ax2.plot(ts, x_as, c='g', label='AnalyticalSol')
ax2.set_xlabel('time step', fontsize='14')
ax2.set_ylabel('deviations', fontsize='14')
ax2.set_title('Analytical: time-specific deviations', fontsize='18')
ax2.grid()
ax2.legend(fontsize='14')

plt.tight_layout()
plt.show()

グラフ

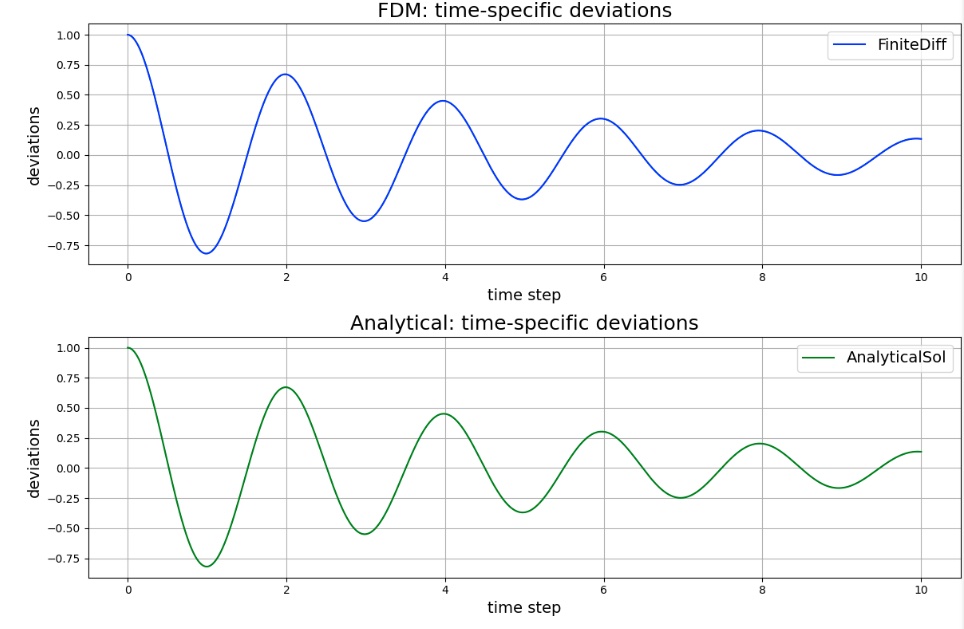
FDM-Analytic

FDMで求めた解は、厳密解と一致していることが分かる。

途中結果をグラフ表示する関数

# Evaluate the model at the appropriate epoch

import matplotlib.pyplot as plt

# Inference using the model trained up to this time
# And draw the results of inference at all times in a graph
def EvalModel(model, t_step, t_data, x_data, epoch):
    # Inference
    x_pred = model(t_step)
    x_pred = x_pred.view(1, -1)[0].to("cpu").detach().numpy()

    # Draw a graph
    fig = plt.figure(figsize=(12,4))
    ax1 = fig.add_subplot(1, 1, 1)
    ax1.plot(ts, x_pred, c='r', label='PINNs')
    ax1.scatter(t_data.to("cpu"), x_data.to("cpu"), label='Training data')
    ax1.set_xlabel('time step', fontsize='14')
    ax1.set_ylabel('deviations', fontsize='14')
    ax1.set_title('PINNs: time-specific deviations at '+str(epoch+1)+' epoch', fontsize='18')
    ax1.grid()
    ax1.legend(fontsize='14')
    plt.tight_layout()
    plt.show()

モデルを定義

# Define fully-connected layer Neural network
#  Input layer: 1
#  Hidden layer: 16, 32, 16
#  Output layer: 1

import torch
from torch import nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(1, 16)  # fully-connected layer
        self.fc2 = nn.Linear(16, 32)
        self.fc3 = nn.Linear(32, 16)
        self.fc4 = nn.Linear(16, 1)

    def forward(self, t):
        x = F.tanh(self.fc1(t))
        x = F.tanh(self.fc2(x))
        x = F.tanh(self.fc3(x))
        x = self.fc4(x)
        return x
    
# run on cuda if possible
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = Net().to(device)

損失関数と最適化関数を定義

from torch import optim

# Loss function: Mean Square Error
loss_func = nn.MSELoss()

# Adam
optimizer = optim.Adam(model.parameters(), lr=1e-3)

観測データ、PINN用に全時間領域分の時間データを準備

観測データとしては、全時間区分（1000データ）の中から「select_data」で示される5つのt_data、およびx_dataは厳密解であるx_asから選択した。微分方程式の誤差を求めるための全時間区分データとして、t_pinnを用意した。

# Prepare data

# Select 5 points from 0 to n_steps-1
#select_data = [0, 200, 500, 700, 900]
#select_data = [0, 150, 250, 350, 550]
select_data = [0, 100, 200, 300, 400]


t_data = torch.tensor(ts[select_data], dtype=torch.float32).view(-1, 1).to(device)
x_data = torch.tensor(x_as[select_data], dtype=torch.float32).view(-1, 1).to(device)

# Prepare time-step data all-over for PINNs

#t_pinn = torch.linspace(0, elasped_t, pinn_step, requires_grad=True).view(-1, 1).to(torch.float32).to(device)
t_pinn = torch.tensor(ts, dtype=torch.float32, requires_grad=True).view(-1, 1).to(device)

学習ループ

「損失関数の考え方」で説明したパラメータについては、先ずは$1$で実行した。

# Train by Physic informed neural network

lambda1 = 1  # weight of physical error (vs. observed data)
epochs = 50000

record_loss = []

for i in range(epochs):
    # 勾配を0に
    optimizer.zero_grad()
    
    # 順伝播
    x_pred = model(t_data)
    loss1 = loss_func(x_pred, x_data)

    # 物理式を計算する
    x_pinn = model(t_pinn)

    x_t = torch.autograd.grad(
        x_pinn,
        t_pinn,
        grad_outputs=torch.ones_like(x_pinn),
        retain_graph=True,
        create_graph=True,
    )[0]
    x_tt = torch.autograd.grad(
        x_t,
        t_pinn,
        grad_outputs=torch.ones_like(x_pinn),
        retain_graph=True,
        create_graph=True,
    )[0]
    f = x_tt + (c/m)*x_t + (k/m)*x_pinn
    loss2 = loss_func(f, torch.zeros_like(f))

    # 誤差を求める
    loss = loss1 + lambda1 * loss2
    record_loss.append(loss.item())
    
    # 逆伝播（勾配を求める）
    loss.backward()
    
    # パラメータの更新
    optimizer.step()

    if i%1000 == 0:
        print("Epoch:", i, "Loss1:", loss1.item(), "loss2:", loss2.item())

    if i%10000 == 0:
        EvalModel(model, t_pinn, t_data, x_data, i)

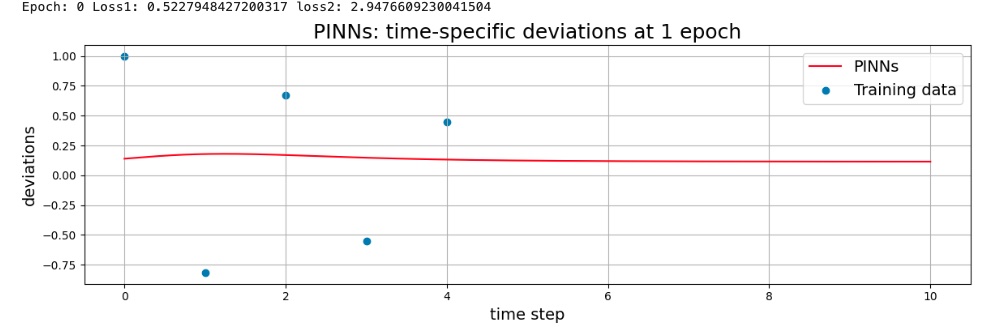
1エポック後のモデル（推論結果グラフ）

pinn1_1

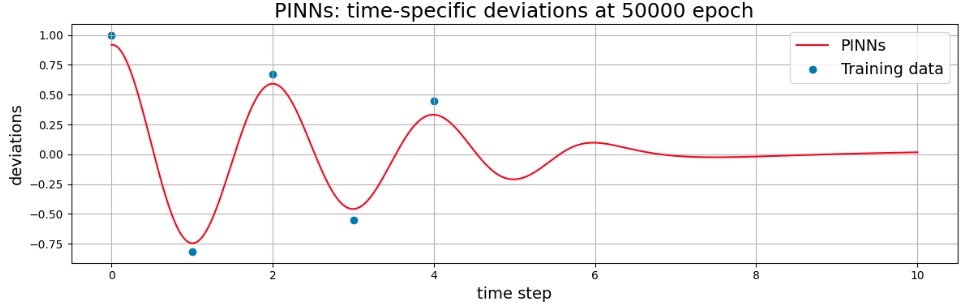
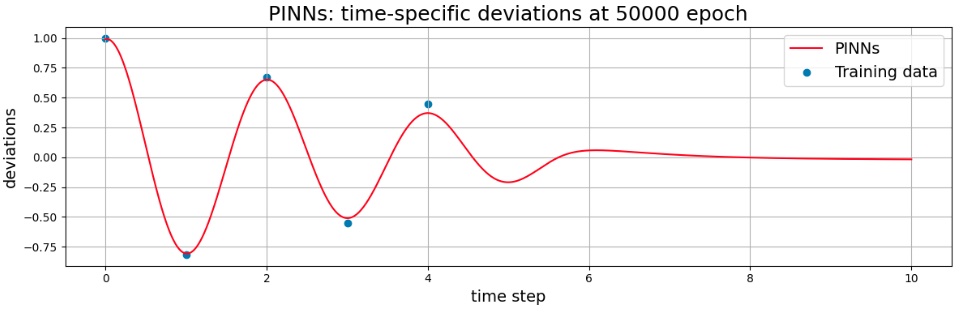
50000エポック後のモデル（推論結果グラフ）

pinn1_50000

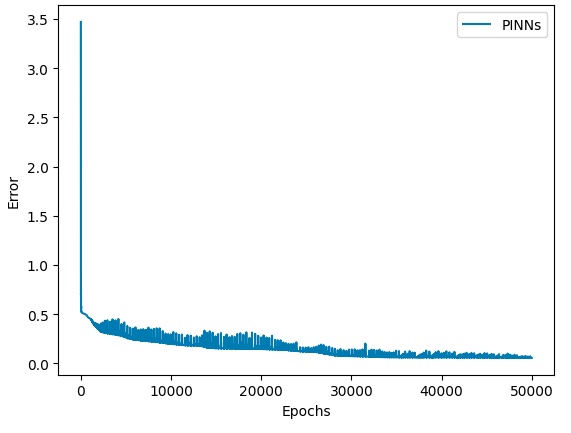
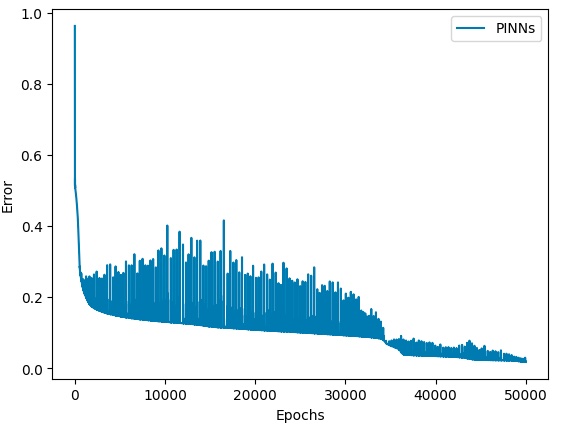
誤差の収束状況

error1

パラメータを見直す

パラメータ変更

学習を進めていくと、観測値（厳密データ）にフィットするように変化するが、50000回回しても観測値には完全に一致しなかった。また、観測値の無い5秒以降、急速に減衰しており、厳密解のような減衰とはなっていない。

そこで、観測値側に寄せるため、物理誤差の効果を弱めるため、パラメータ$\lambda_{1}$を$0.2$として実行した。

50000エポック後のモデル（推論結果グラフ）

pinn02_50000

誤差の収束状況

error02

まとめ

PINNsの考え方は多少なりとも理解できたが、PINNsで50000回の学習を行ったモデルを使って推論した結果は、厳密解とは一致しなかった。コードの見直しを何度も行ったが、現時点では原因は不明である。

また、別の問題をPINNsで挑戦して、更に理解を深めると分かるのかもしれない。