はじめに
先日、PINNsで質点・ばね・ダンパー問題をまとめた。今回はバーガース方程式を取り組んだので、その内容をまとめた。
情報源
- Solving 1D Burgers’ Equation - Finite Difference vs Neural Network - FDM(有限差分法)とPINNsの2つの手法でバーガース方程式を解いている。このページは今回非常に参考になった。
- PytorchでPhysics-Informed Neural Networkを実装する ①バーガース方程式 - PINNs実装面でコードを参考にした。PINNs初期状態をプロットする部分このページによるところ大である。
- pinn_burgers - このページでは、optimizerとして記憶制限BFGS法(BFGS法は準ニュートン法の解法の一つ)を使っている。
- Physics Informed Deep Learning (Part I) - PINNsの有効性についての論文。情報源3.からも参照されている。こちらがPart II。自分はPart IもPart IIも読んでいない。
物理的背景
コードを理解するために、物理的背景を先ずはまとめる。数学的な厳密性を欠いてはいるが、要点は整理できていると思っている。
微分方程式
$u(x, t)$で表現される場を考え、$\nu$を動粘性率(kinematic viscosity)とすると、バーガース方程式は次式で与えられる。 $$ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} =\nu\frac{\partial^{2}u}{\partial x^{2}} \tag{1} $$
有限差分法
先ず、関数$f(x)$において、$x+\Delta x$と$x-\Delta x$でテーラー展開すると、次のように表せる。 $$ f(x+\Delta x)=f(x)+\frac{\partial f(x)}{\partial x}\Delta x +\frac{1}{2!}\frac{\partial^{2}f(x)}{\partial x^{2}}\Delta x^{2} + \frac{1}{3!}\frac{\partial^{3}f(x)}{\partial x^{3}}\Delta x^{3} + \cdots \tag{2} $$ $$ f(x-\Delta x)=f(x)-\frac{\partial f(x)}{\partial x}\Delta x +\frac{1}{2!}\frac{\partial^{2}f(x)}{\partial x^{2}}\Delta x^{2} - \frac{1}{3!}\frac{\partial^{3}f(x)}{\partial x^{3}}\Delta x^{3} + \cdots \tag{3} $$
(2)式、(3)式を参考に、関数$u(x,t)$について、$u_{i-1}, u_i, u_{i+1}$は次のように書ける。 $$ u_{i+1} = u_i + \Delta x \frac{\partial u}{\partial x} |_i + \frac{\Delta x^2}{2}\frac{\partial^2 u}{\partial x^2}|_i + \frac{\Delta x^3}{6}\frac{\partial^3 u}{\partial x^3}|i + \mathcal{O}(\Delta x^4) \tag{4} $$ $$ u{i-1} = u_i - \Delta x \frac{\partial u}{\partial x} |_i + \frac{\Delta x^2}{2}\frac{\partial^2 u}{\partial x^2}|_i - \frac{\Delta x^3}{6}\frac{\partial^3 u}{\partial x^3}|_i + \mathcal{O}(\Delta x^4) \tag{5} $$
(4)式と(5)式の和は、次の通り。 $$ u_{i-1}+u_{i+1} = 2u_i +\Delta x^2\frac{\partial^2 u}{\partial x^2}|i + \mathcal{O}(\Delta x^4) \tag{6} $$ 高次の項を無視すると、次が導き出せる。 $$ \frac{\partial^2 u}{\partial x^2} = \frac{u{i-1} - 2u_i + u_{i+1}}{\Delta x^2} \tag{7} $$ ここで、物理量$u$を時間微分は、次式の極限として定義される。 $$ \frac{\partial u}{\partial t} = \lim_{\Delta x \rightarrow 0}\frac{u(x+\Delta t)-u(x)}{\Delta t} \tag{8} $$ (8)式において、$\Delta t$を微小量とすると、近似として次の通りとなる。 $$ \frac{\partial u}{\partial t} \approx \frac{u(x+\Delta t)-u(x)}{\Delta t} \tag{9} $$ バーガース方程式(1)は、(7)、(9)式を使って、離散表現すると、次の通り。 $$ \frac{u_i^{n+1} - u_i^n}{\Delta t} + u_i^n\frac{u_i^n - u_{i-1}^n}{\Delta x} = \nu\frac{u_{i+1}^n -2u_i^n + u_{i-1}^n}{\Delta x^2} \tag{10} $$ ここで、$u^{n+1}$は、$u^n$から時間が1つ進んだ時の関数を表す。
(10)式を$u_i^{n+1}$で解くと次の通り。 $$ u_i^{n+1} = u_i^n - u_i^n\frac{\Delta t}{\Delta x}(u_i^n - u_{i-1}^n) + \frac{\nu \Delta t}{\Delta x^2}(u_{i+1}^n -2u_i^n + u_{i-1}^n) \tag{11} $$ (11)式は、$u^n$の時の関数値から次の時間ステップに進めるための式である。
PINNs
ニューラルネットワークを関数$NN(x)$とし、バーガース方程式を表現する関数$NN(x,t)$を考える。
普遍性定理(Universal Approximation Theorem)によると、ニューラルネットワークは、任意の連続関数を近似可能であるから、バーガース方程式は、次のニューラルネットワークで表すことができる。 $$ u(x,t) \approx NN(x,t) \tag{12} $$ 関数$NN(x,t)$の微分係数を$\frac{\partial NN}{\partial t}, \frac{\partial^2 NN}{\partial x^2}$等とすると、(1)のバーガース方程式は、次の通りである。 $$ f(x,t) = \frac{\partial NN}{\partial t} + NN \frac{\partial NN}{\partial x} - \nu \frac{\partial^2 NN}{\partial x^2} = 0 \tag{13} $$ PINNsでは上記を支配方程式と呼ばれている。この支配方程式の誤差を最小化していく。
コード
パッケージ(ライブラリ)を取り込む
# Import packages
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import optim
from torch.optim import lr_scheduler
import matplotlib.pyplot as plt
from matplotlib import cm
# run on cuda if possible
device = 'cuda' if torch.cuda.is_available() else 'cpu'
定数を定義
# Define constants
# Define the spatio-temporal extent of the problem domain
# x∈[0,2] t∈[0,0.48]
x_min = 0
x_max = 2
t_min = 0
t_max = 0.48
x_total = 1000
t_total = 1000
dx = (x_max - x_min)/x_total
dt = (t_max - t_min)/t_total
# kinematic viscosity
k_vis = 0.01/np.pi
# For subsequent calculations,
# create a grid of the spatio-temporal region in question.
x = torch.linspace(x_min, x_max, x_total).view(-1,1)
t = torch.linspace(t_min, t_max, t_total).view(-1,1)
X, T = torch.meshgrid(x.squeeze(1),t.squeeze(1), indexing='ij')
初期条件、境界条件を定義
# Initial condition: u=sin(πx) when t= 0, x∈[0,2]
X_init = torch.hstack((X[:,0][:,None], T[:,0][:,None]))
U_init = torch.sin(np.pi*X_init[:,0]).unsqueeze(1)
# Boundary condition: u=0 when x=0, x=2, t∈[0,0.48]
X_bottom = torch.hstack((X[0,:][:,None], T[0,:][:,None]))
X_top = torch.hstack((X[-1,:][:,None], T[-1,:][:,None]))
U_bottom = torch.zeros(X_bottom.shape[0],1)
U_top = torch.zeros(X_top.shape[0],1)
X_bc = torch.vstack([X_bottom, X_top])
U_bc = torch.vstack([U_bottom, U_top])
有限差分法で解く(可視化1)
# FDM Function for Burgers' equation
def FDM(st):
x_num = st.shape[0]
t_num = st.shape[1]
for j in range(1, t_num):
for i in range(1, x_total-1):
x = st[:,j-1]
st[i, j] = x[i] - x[i]*(dt/dx)*(x[i]-x[i-1]) + k_vis*dt/(dx*dx)*(x[i+1]-2*x[i]+x[i-1])
# Draw contour plots of u(x,t) for all regions of a given time and space
def plot3d(x, t, u):
X, T = np.meshgrid(x, t, indexing='ij')
fig = plt.figure(figsize=(12,12))
ax1 = fig.add_subplot(2, 1, 1)
cp = ax1.contourf(T, X, u, 20, cmap=cm.rainbow)
fig.colorbar(cp)
ax1.set_title('u')
ax1.set_xlabel('t')
ax1.set_ylabel('x')
ax2 = fig.add_subplot(2, 1, 2, projection='3d')
surf = ax2.plot_surface(T, X, u, cmap=cm.rainbow, antialiased=False)
ax2.set_xlabel('t')
ax2.set_ylabel('x')
ax2.set_zlabel('u')
plt.tight_layout()
plt.show()
# Prepare a 2-dimensional array to store u(x,t)
# And set initial condition
st = np.zeros([x_total, t_total]) # array[space, time]
st[:,0] = U_init[:,0]
# Solve Burgers' equation with Finite Differential Method
FDM(st)
u_fdm = st # Save for comparison with PINNs
plot3d(X[:,0], T[0,:], st)
初期条件・境界条件から、使用する部分を選ぶ
# Select the number of pieces specified from the initial and boundary conditions
# Define the number of pieces to be selected
N_ic = 1000
N_bc = 1000
idx = np.random.choice(X_init.shape[0], N_ic, replace=False)
X_ic_select = X_init[idx, :].to(device)
U_ic_select = U_init[idx, :].to(device)
idx = np.random.choice(X_bc.shape[0], N_bc, replace=False)
X_bc_select = X_bc[idx, :].to(device)
U_bc_select = U_bc[idx, :].to(device)
初期条件については、「x_total」と「N_ic」の値の関係から分かる通り、当初作成したデータの全てを使用している。
PINNsを評価するためのデータセットを作成
# Create a test set from u(x,t) obtained by FDM
# to evaluate the model in the middle of training
x_test = torch.hstack((X.transpose(1,0).flatten()[:,None],
T.transpose(1,0).flatten()[:,None])).to(device)
u_test = torch.from_numpy(u_fdm.transpose(1,0).flatten()[:,None]).float().to(device)
上記のデータは、PINNsを使って学習しているモデルを評価するためテストデータセットである。正解データは、FDMで作られたデータを使う。
PINNsの計算対象領域用のデータを作成
(13)式を評価(誤差を最小化)するためのデータセットを作成する。最終的には、初期条件、境界条件も加える。
# Coordinates of the computational domain
# in which the PINNs' loss is evaluated: x ∈ [0,2], t ∈ [0,0.48]
n_domain = 10000
t_domain = torch.rand(n_domain) * t_max
x_domain = torch.rand(n_domain) * x_max
X_train = torch.stack([x_domain, t_domain], dim=0).T.to(device)
X_train_final = torch.vstack((X_train, X_ic_select, X_bc_select))
初期条件・境界条件、評価領域を可視化(可視化2)
# Graph the status before starting
fig = plt.figure(figsize=(12,12))
ax1 = fig.add_subplot(2, 1, 1)
ax1.set_xlim(t_min, t_max)
ax1.set_title('Initial Status of Computational Domain')
ax1.set_xlabel('t')
ax1.set_ylabel('x')
cp = ax1.scatter(X_ic_select[:,1].to("cpu"), X_ic_select[:,0].to("cpu"), c=U_ic_select.to("cpu"), cmap=cm.rainbow, s=50) # initial condition
fig.colorbar(cp)
ax1.scatter(X_bc_select[:,1].to("cpu"), X_bc_select[:,0].to("cpu"), c=U_bc_select.to("cpu"), s=10) # boundary condition
ax1.scatter(X_train[:,1].to("cpu"), X_train[:,0].to("cpu"), c='gray', s=10) # computational domain
ax2 = fig.add_subplot(2, 1, 2)
ax2.scatter(X_ic_select[:,0].to("cpu"), U_ic_select.to("cpu"), c=U_ic_select.to("cpu"), cmap=cm.rainbow, s=10)
ax2.set_title('Burgers\' Equation at t=0')
ax2.set_xlabel('x')
ax2.set_ylabel('u')
plt.tight_layout()
plt.show()
ニューラルネットワークを定義
# define u_NN class
class u_NN(nn.Module):
def __init__(self, n_input, n_output, n_hiddens=[32,64,128,128,64,32]):
super().__init__()
self.activation = nn.Tanh()
self.input_layer = nn.Linear(n_input, n_hiddens[0])
self.hidden_layers = nn.ModuleList(
[nn.Linear(n_hiddens[i], n_hiddens[i+1]) for i in range(len(n_hiddens)-1)]
)
self.output_layer = nn.Linear(n_hiddens[-1], n_output)
def forward(self, x):
x = self.activation(self.input_layer(x))
for layer in self.hidden_layers:
x = self.activation(layer(x))
x = self.output_layer(x)
return x
def loss_bc(self, x_bc, u_bc):
u_pred = self.forward(x_bc)
l_bc = loss_func(u_pred, u_bc)
return l_bc
def loss_ic(self, x_ic, u_ic):
u_pred = self.forward(x_ic)
l_ic = loss_func(u_pred, u_ic)
return l_ic
def loss_pinn(self, x):
x_clone = x.clone()
x_clone.requires_grad = True
NN = self.forward(x_clone)
NNx_NNt = torch.autograd.grad(
NN,
x_clone,
torch.ones([x_clone.shape[0], 1]).float().to(device),
retain_graph=True,
create_graph=True,
)[0]
NNxx_NNtt = torch.autograd.grad(
NNx_NNt,
x_clone,
torch.ones(x_clone.shape).float().to(device),
create_graph=True,
)[0]
NNt = NNx_NNt[:,[1]] # dt term
NNx = NNx_NNt[:,[0]] # dx term
NNxx = NNxx_NNtt[:,[0]] # dx^2 term
f = NNt + self.forward(x_clone)*(NNx) + k_vis*NNxx
zeros = torch.zeros(f.shape[0],1).float().to(device)
l_pinn = loss_func(f, zeros)
return l_pinn
def total_loss(self, x_ic, u_ic, x_bc, u_bc, x):
l_bc = self.loss_bc(x_bc, u_bc)
l_ic = self.loss_ic(x_ic, u_ic)
l_pinn = self.loss_pinn(x)
return l_bc+l_ic+l_pinn
PINN = u_NN(2, 1).to(device)
「loss_pinn」の微分係数を求める部分は、自身がコーディングするも上手くいかず、情報源1.から流用した。
その部分が今回の問題の肝の部分だと思う。
定義したモデルの構造は次の通りである。
u_NN(
(activation): Tanh()
(input_layer): Linear(in_features=2, out_features=32, bias=True)
(hidden_layers): ModuleList(
(0): Linear(in_features=32, out_features=64, bias=True)
(1): Linear(in_features=64, out_features=128, bias=True)
(2): Linear(in_features=128, out_features=128, bias=True)
(3): Linear(in_features=128, out_features=64, bias=True)
(4): Linear(in_features=64, out_features=32, bias=True)
)
(output_layer): Linear(in_features=32, out_features=1, bias=True)
)
誤差関数、オプティマイザーを定義
from torch import optim
# Loss function: Mean Square Error
loss_func = nn.MSELoss()
# Optimizer: Adam(Adaptive moment estimation)
optimizer = optim.Adam(PINN.parameters(), lr=0.001)
scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=0.98)
学習ループ
# Learning Loop
num_epoch = 20000 # epoch count
# List Variables for Recording
Epoch = []
Learning_Rate = []
IC_loss = []
BC_loss = []
PINN_loss = []
Total_loss = []
Test_loss = []
for i in range(num_epoch):
if i == 0:
print("Epoch \t Learning-Rate \t IC_Loss \t BC_Loss \t PINN_Loss \t Total_Loss \t Test_Loss")
l_ic = PINN.loss_ic(X_ic_select, U_ic_select)
l_bc = PINN.loss_bc(X_bc_select, U_bc_select)
l_pinn = PINN.loss_pinn(X_train_final)
loss = PINN.total_loss(X_ic_select, U_ic_select, X_bc_select, U_bc_select, X_train_final)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i % 100 == 0:
with torch.no_grad():
test_loss = PINN.loss_bc(x_test,u_test)
Epoch.append(i)
Learning_Rate.append(scheduler.get_last_lr()[0])
IC_loss.append(l_ic.detach().cpu().numpy())
BC_loss.append(l_bc.detach().cpu().numpy())
PINN_loss.append(l_pinn.detach().cpu().numpy())
Total_loss.append(loss.detach().cpu().numpy())
Test_loss.append(test_loss.detach().cpu().numpy())
if i % 1000 == 0:
print(i, "\t",
format(scheduler.get_last_lr()[0], ".4E"), "\t",
format(l_ic.detach().cpu().numpy(), ".4E"), "\t",
format(l_bc.detach().cpu().numpy(), ".4E"), "\t",
format(l_pinn.detach().cpu().numpy(), ".4E"), "\t",
format(loss.detach().cpu().numpy(), ".4E"), "\t",
format(test_loss.detach().cpu().numpy(), ".4E"), "\t",
)
scheduler.step()
学習したモデルを評価(可視化3)
# Inference the entire domain of a given time and space
# using the model learned for evaluation
x_mesh = np.linspace(x_min, x_max, x_total)
t_mesh = np.linspace(t_min, t_max, t_total)
X_mesh, T_mesh = np.meshgrid(x_mesh, t_mesh)
# Inference
X = X_mesh.reshape(-1, 1)
T = T_mesh.reshape(-1, 1)
Y = np.block([X, T])
Y = torch.tensor(Y, requires_grad=True, dtype=torch.float32).to(device)
U = PINN(Y)
st = U.view(-1, 1).to("cpu").detach().numpy()
st = np.reshape(st, (t_total, x_total)).T # Transposition as it can be packed in the column direction.
推論結果である「U」(列ベクトル)を2次元の「st」にreshapeする時に、列方向に埋められていくことに気づかず、転置を忘れていて少しハマった。
# Draw contour plots of u(x,t) for all regions of a given time and space
# using trained model
u_pinn = U.reshape(t_total,x_total).T.detach().to("cpu").numpy()
plot3d(x_mesh, t_mesh, u_pinn)
PINNsとFDMとの差異(可視化4)
# Displays the difference between FDM and PINNs
plot3d(x_mesh, t_mesh, (u_pinn-u_fdm))
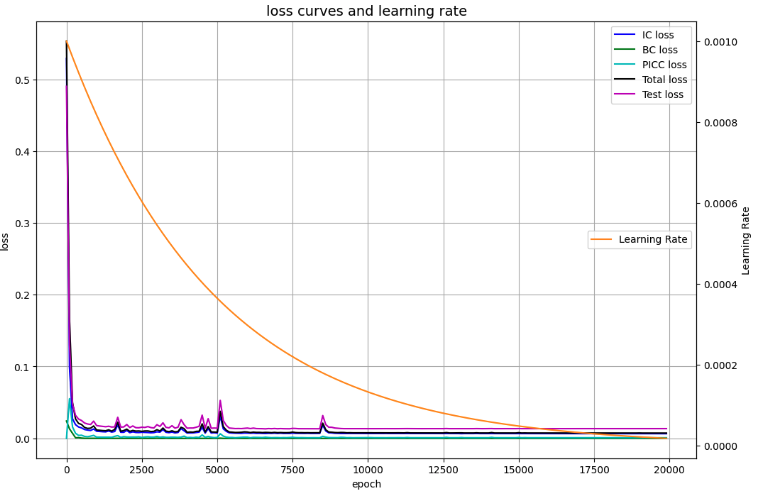
誤差の収束状況を可視化(可視化5)
# Draw loss curves
fig, ax1 = plt.subplots(figsize=(12, 8))
ax2 = ax1.twinx()
ax1.plot(Epoch, IC_loss, c='b', label='IC loss')
ax1.plot(Epoch, BC_loss, c='g', label='BC loss')
ax1.plot(Epoch, PINN_loss, c='c', label='PICC loss')
ax1.plot(Epoch, Total_loss, c='k', label='Total loss')
ax1.plot(Epoch, Test_loss, c='m', label='Test loss')
ax1.set_xlabel('epoch')
ax1.set_ylabel('loss')
ax1.set_title('loss curves and learning rate', fontsize='14')
ax1.grid()
ax1.legend(loc=1)
ax2.plot(Epoch, Learning_Rate, c='darkorange', label='Learning Rate')
ax2.set_ylabel('Learning Rate')
ax2.legend(loc=7)
plt.show()
可視化結果
コードのタイトルと「可視化n」で対応付けている。
FDMの結果(可視化1)
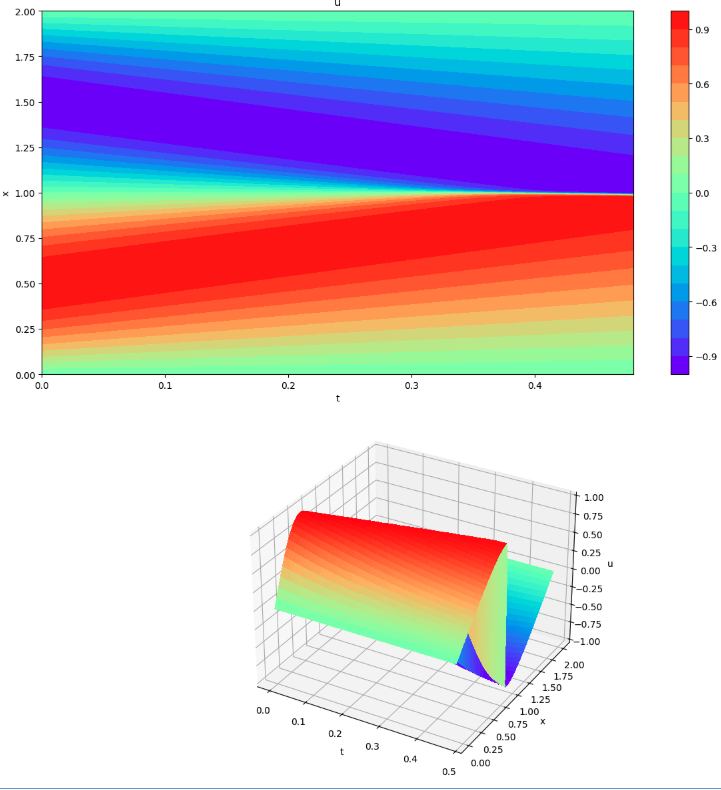
PINNs開始前の状態(可視化2)
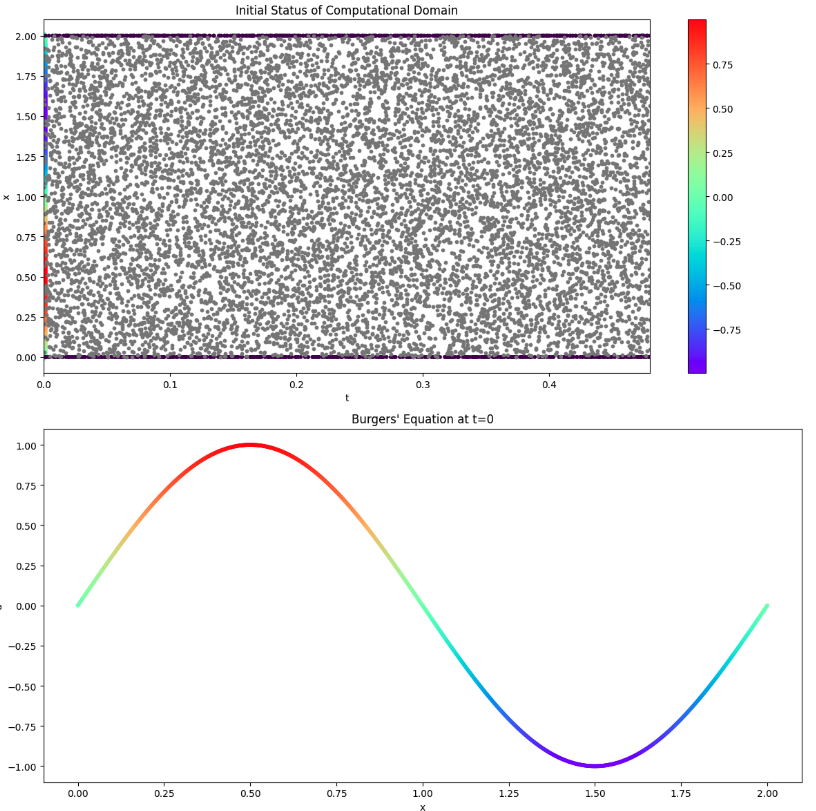
学習モデルを評価(可視化3)
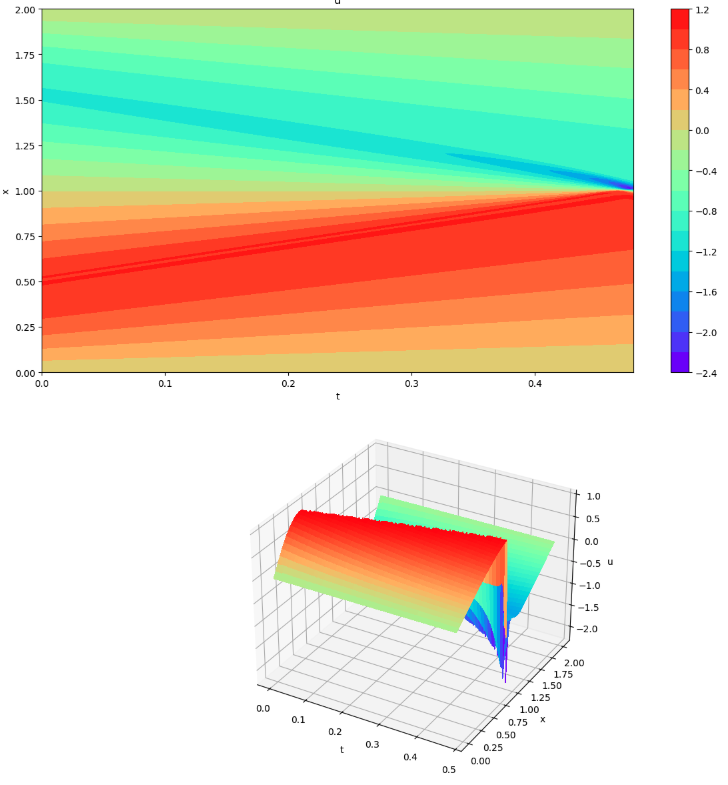
PINNsとFDMの差異(可視化4)
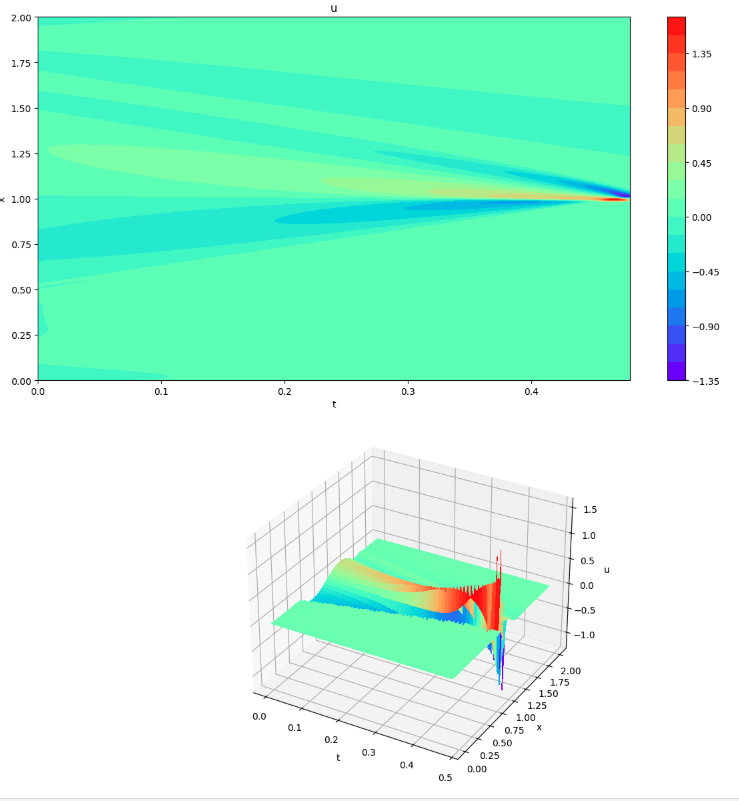
誤差の収束状況(可視化5)
まとめ
今回の経験を通じて、PINNsの振る舞いについて理解が深まった。またコーディングで苦労した(ハマった)ことで、Python、 PyTorchについて(特に、Tensor、配列の次元、自動微分など)が少しは分かるようになった。
PINNsについて、コードの難易度、実行時間(求解までの所要時間)をFDMと比較すると、その優位性についてはまだ理解が出来ていない。
自分が興味ある天文(天体物理、宇宙物理)に関連する現象で、PINNsを試してみたいと思っている。