はじめに
前回の投稿では、論文の内容を参考に遷移状態のLaminar Flowについて、VP型の支配方程式を使ってPINNsで再現するも、参考論文の値と大きく異なった結果となったことを述べた。今回ST型の支配方程式でも実施したので、その結果をこの投稿でまとめる。
情報源
- PINN-laminar-flow/PINN_unsteady - これまでも情報源として参考にしてきた論文とgithub。この論文のCauchy stress tensorの部分(連続体力学に基づく定式化)、すなわち式(3)(4)でつまづいていた。
- On Physics-Informed Deep Learning for Solving Navier-Stokes Equations - このページから参照される論文に、Navier-Stokes方程式の2つの型(VP formとST form)についての記載がある。但し、この論文の課題設定は、定常状態を扱っており、時間変数$t$は含まれていない。
物理的背景
VP型、ST型については、こちらの投稿を参考にして欲しい(参考論文へのリンクあり)。
Cauchy stress tensor (ST) form
情報源1.の式(3)(4)を支配方程式としてコーディングするため2次元成分表記に表そうとした。しかし、それが出来なかったので、情報源1.のGithubのコードを読み、次の支配方程式を得た。自分がつまづいていた情報源1.の式(3)(4)は、次の通り。 $$ \frac{\partial \boldsymbol{v}}{\partial t} + (\boldsymbol{v}\cdot\nabla)\boldsymbol{v} = \frac{1}{\rho}\nabla\cdot\boldsymbol{\sigma} + \boldsymbol{g} \tag{1} $$ $$ \boldsymbol{\sigma} = -p\boldsymbol{I} + \mu(\nabla\boldsymbol{v}+\nabla\boldsymbol{v}^{T}) \tag{2} $$
今回PINNsで使うニューラルネットを関数p_NN()とすると、p_NN()は時空間変数を混合変数へと写像する関数である。次のように表される。 $$ (x, y, t) \longmapsto (\psi, p, \sigma_{11}, \sigma_{22}, \sigma_{12}) \tag{3} $$ ここで、$\psi$は流線関数であり、流速は$u = \frac{\partial \psi}{\partial y}$、$v = - \frac{\partial \psi}{\partial x}$となる。これにより連続方程式は自動的に満たされるとのこと(情報源1.の論文より)。$p$は圧力である。$\sigma_{11},\sigma_{22},\sigma_{12}$を使って支配方程式を以下に示す。以下の表記において、例えば$\partial_t u$は$\frac{\partial u}{\partial t}$を表す。 $$ f_u = \rho \partial_t u + \rho(u\partial_x u + v\partial_y u) - \partial_x \sigma_{11} - \partial_y \sigma_{12} \tag{4} $$
$$ f_v = \rho \partial_t v + \rho(u\partial_x v + v\partial_y v) - \partial_x \sigma_{12} - \partial_y \sigma_{22} \tag{5} $$
$$ f_{xx} = -p + 2\mu\partial_x u - \sigma_{11} \tag{6} $$
$$ f_{yy} = -p + 2\mu\partial_y v - \sigma_{22} \tag{7} $$
$$ f_{xy} = \mu(\partial_y u + \partial_x v) - \sigma_{12} \tag{8} $$
$$ f_p = p + \frac{1}{2}(\sigma_{11}+\sigma_{22}) \tag{9} $$
式(3)の損失関数として、それらを最小化する方向に学習を進めて行けば、問題としている環境(領域、境界条件)を表すニューラルネット上に表現された関数p_NN()となる。
コード
前回のこの投稿と異なる部分のみを掲載する。
全結合層のネットワーククラスを作成
# define p_NN class
class p_NN(nn.Module):
def __init__(self, n_input, n_output, n_hiddens=[32,64,128,128,64,32]):
super().__init__()
self.activation = nn.Tanh()
self.input_layer = nn.Linear(n_input, n_hiddens[0])
self.hidden_layers = nn.ModuleList(
[nn.Linear(n_hiddens[i], n_hiddens[i+1]) for i in range(len(n_hiddens)-1)]
)
self.output_layer = nn.Linear(n_hiddens[-1], n_output)
def forward(self, x):
x = self.activation(self.input_layer(x))
for layer in self.hidden_layers:
x = self.activation(layer(x))
x = self.output_layer(x)
return x
def neural_net(self, x, y, t):
inputs = torch.cat([x, y, t], dim=1)
outputs = self.forward(inputs)
psi = outputs[:, 0:1]
p = outputs[:, 1:2]
s11 = outputs[:, 2:3]
s22 = outputs[:, 3:4]
s12 = outputs[:, 4:5]
return psi, p, s11, s22, s12
def net_uvp(self, x, y, t):
x.requires_grad = True
y.requires_grad = True
t.requires_grad = True
psi, p, s11, s22, s12 = self.neural_net(x, y, t)
u = gradients(psi, y)
v = -gradients(psi, x)
return u, v, p, s11, s22, s12
def net_f(self, x, y, t):
u, v, p, s11, s22, s12 = self.net_uvp(x, y, t)
u_x = gradients(u, x)
u_y = gradients(u, y)
u_t = gradients(u, t)
s11_x = gradients(s11, x)
s12_y = gradients(s12, y)
fu = rho*u_t + rho*(u*u_x + v*u_y) - (s11_x + s12_y)
v_x = gradients(v, x)
v_y = gradients(v, y)
v_t = gradients(v, t)
s12_x = gradients(s12, x)
s22_y = gradients(s22, y)
fv = rho*v_t + rho*(u*v_x + v*v_y) - (s12_x + s22_y)
fxx = -p + mu*2.0*u_x - s11
fyy = -p + mu*2.0*v_y - s22
fxy = mu*(u_y + v_x) - s12
fp = p + (s11 + s22)/2.0
return fu, fv, fxx, fyy, fxy, fp
def predict(self, x, y, t): # no tensor is passed, return no tensor
xx = torch.tensor(x, device=device, dtype=torch.float32)
yy = torch.tensor(y, device=device, dtype=torch.float32)
tt = torch.tensor(t, device=device, dtype=torch.float32)
uu, vv, pp, _, _, _ = self.net_uvp(xx, yy, tt)
u = uu.to("cpu").detach().numpy()
v = vv.to("cpu").detach().numpy()
p = pp.to("cpu").detach().numpy()
return u, v, p
「物理的背景」で説明した支配方程式を適用するために、neural_net()、net_uvp()およびnet_f()のみを変更した。これらの関数を呼んでいる箇所の引数受け取り部分も変更している。
損失関数、最適化関数を定義
# Loss function: Mean Square Error
loss_func = nn.MSELoss()
# Optimizer: Adam(Adaptive moment estimation)
optimizer = optim.Adam(model.parameters(), lr=0.0005)
# scheduler = lr_scheduler.ExponentialLR(optimizer, gamma=0.98)
今回、学習率は情報源1.に併せ、0.0005とした。
学習ループ
# learning Loop
num_epoch = 30000 # epoch count
Epoch = []
Loss_fv = []
Loss_fu = []
Loss_fxx = []
Loss_fyy = []
Loss_fxy = []
Loss_fp = []
Loss_PINN = []
Loss_TOTAL = []
Loss_IC = []
Loss_WALL = []
Loss_INLET = []
Loss_OUTLET = []
for i in range(num_epoch):
if i == 0:
print("Epoch \t Loss_Total \t Loss_PINN \t Loss_IC \t Loss_WALL \t Loss_INLET \t Loss_OUTLET")
optimizer.zero_grad()
fu, fv, fxx, fyy, fxy, fp = model.net_f(x_c, y_c, t_c)
loss_fu = torch.mean(fu**2)
loss_fv = torch.mean(fv**2)
loss_fxx = torch.mean(fxx**2)
loss_fyy = torch.mean(fyy**2)
loss_fxy = torch.mean(fxy**2)
loss_fp = torch.mean(fp**2)
loss_PINN = loss_fu + loss_fv + loss_fxx + loss_fyy + loss_fxy + loss_fp
u_ic, v_ic, p_ic, _, _, _ = model.net_uvp(x_IC, y_IC, t_IC)
loss_IC = torch.mean(u_ic**2) + torch.mean(v_ic**2) + torch.mean(p_ic**2)
u_wall, v_wall, _, _, _, _ = model.net_uvp(x_WALL, y_WALL, t_WALL)
loss_WALL = torch.mean(u_wall**2) + torch.mean(v_wall**2)
u_inlet, v_inlet, _, _, _, _ = model.net_uvp(x_INLET, y_INLET, t_INLET)
loss_INLET = torch.mean((u_inlet - u_INLET)**2) + torch.mean(v_inlet**2)
_, _, p_outlet, _, _, _ = model.net_uvp(x_OUTLET, y_OUTLET, t_OUTLET)
loss_OUTLET = torch.mean(p_outlet**2)
loss_TOTAL = loss_PINN + loss_IC + 5*loss_WALL + 5*loss_INLET + loss_OUTLET
loss_TOTAL.backward()
optimizer.step()
if i % 100 == 0:
Epoch.append(i)
Loss_fu.append(loss_fu.detach().cpu().numpy())
Loss_fv.append(loss_fv.detach().cpu().numpy())
Loss_fxx.append(loss_fxx.detach().cpu().numpy())
Loss_fyy.append(loss_fyy.detach().cpu().numpy())
Loss_fxy.append(loss_fxy.detach().cpu().numpy())
Loss_fp.append(loss_fp.detach().cpu().numpy())
Loss_PINN.append(loss_PINN.detach().cpu().numpy())
Loss_TOTAL.append(loss_TOTAL.detach().cpu().numpy())
Loss_IC.append(loss_IC.detach().cpu().numpy())
Loss_WALL.append(loss_WALL.detach().cpu().numpy())
Loss_INLET.append(loss_INLET.detach().cpu().numpy())
Loss_OUTLET.append(loss_OUTLET.detach().cpu().numpy())
if i % 1000 == 0:
print(i, "\t",
format(loss_TOTAL.detach().cpu().numpy(), ".4E"), "\t",
format(loss_PINN.detach().cpu().numpy(), ".4E"), "\t",
format(loss_IC.detach().cpu().numpy(), ".4E"), "\t",
format(loss_WALL.detach().cpu().numpy(), ".4E"), "\t",
format(loss_INLET.detach().cpu().numpy(), ".4E"), "\t",
format(loss_OUTLET.detach().cpu().numpy(), ".4E"), "\t",
)
上記の学習ループ部分では、net_f()のリターン値を受け取る部分、それらから支配方程式のロスを計算する部分、およびneural_net()を呼ぶ箇所をnet_uvp()に変更した。これらの変更は支配方程式変更に対応したものである。
情報源1.に併せ、全損失を求める箇所で、WALLとINLETに重み付けをした。
学習が充分に進んだ結果を得るため、学習ループを50,000回に増やした。
可視化結果
ST型による結果
学習状況
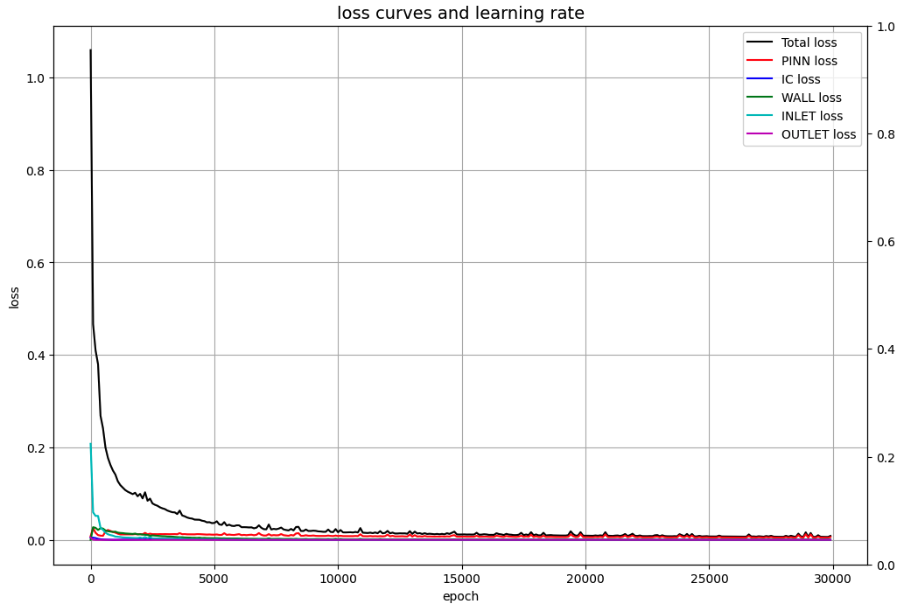
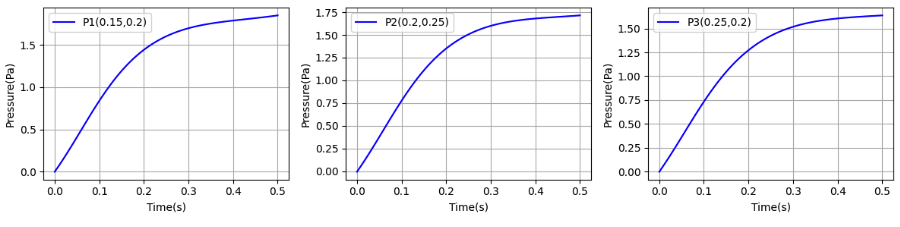
特定地点の圧力推移
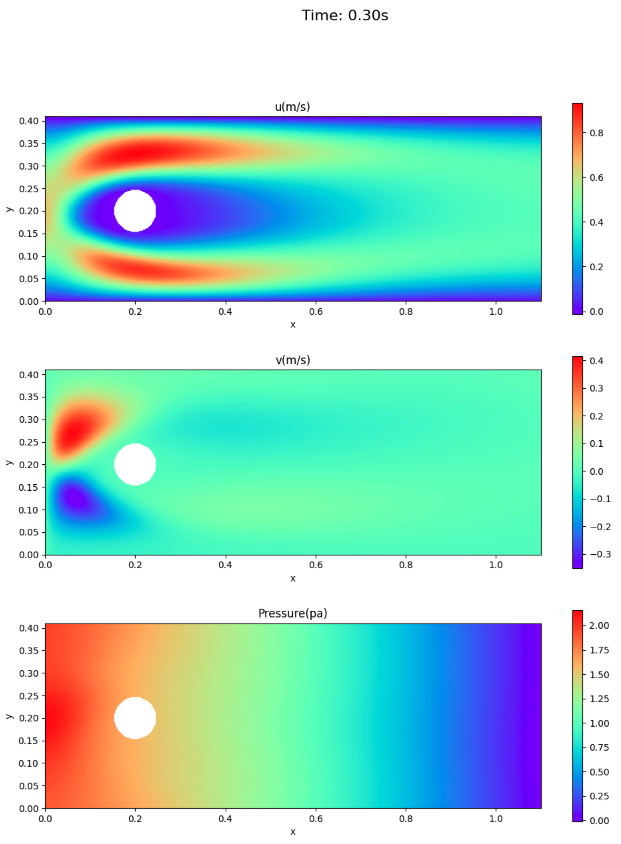
速度場と圧力場
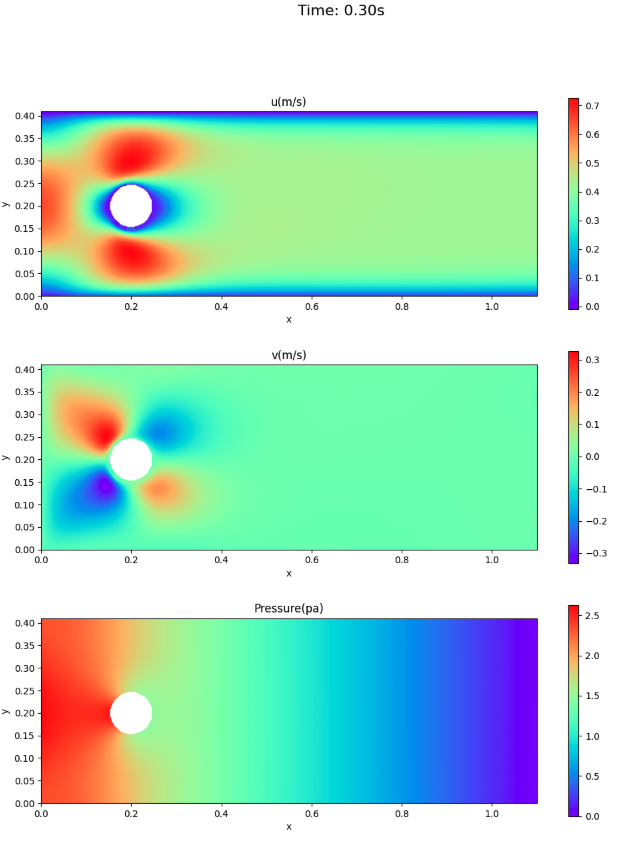
ここでは、アニメーションでなく、論文との比較のため、時刻0.3秒と0.5秒における速度場・圧力場を示す。
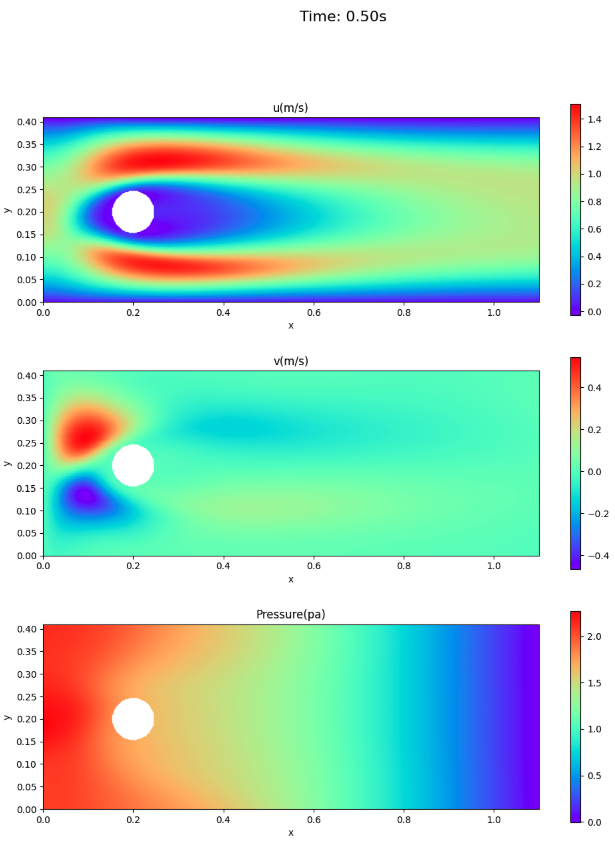
VP型による結果
参考のため、同じ条件(学習率、損失の重み付け、50,000回ループ)で、VP型(学習率、損失の重み付け、50,000回ループ以外の箇所は、前回と同じコード)での結果も示す。
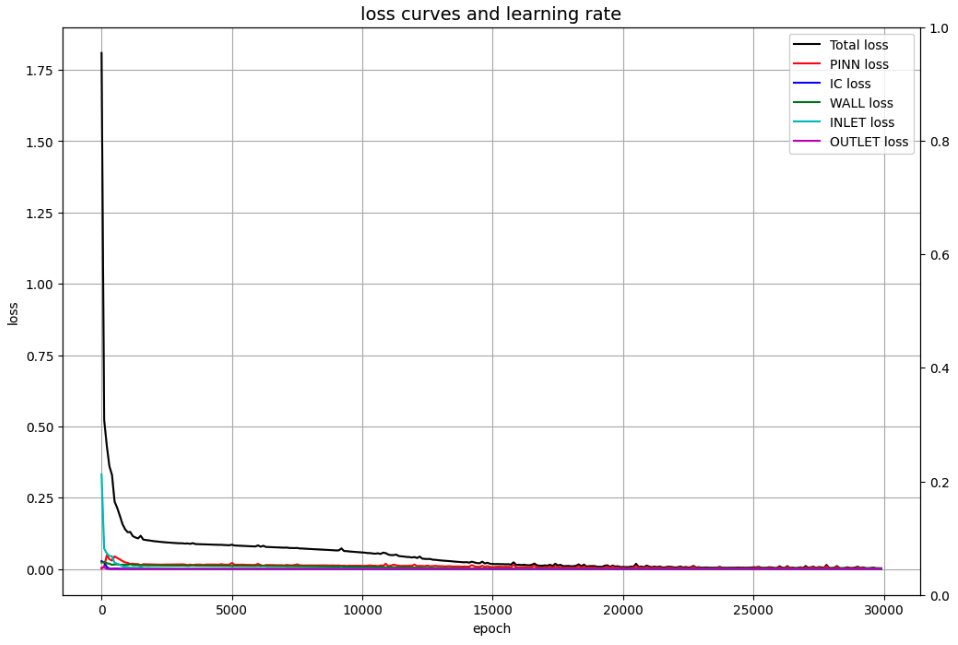
学習状況
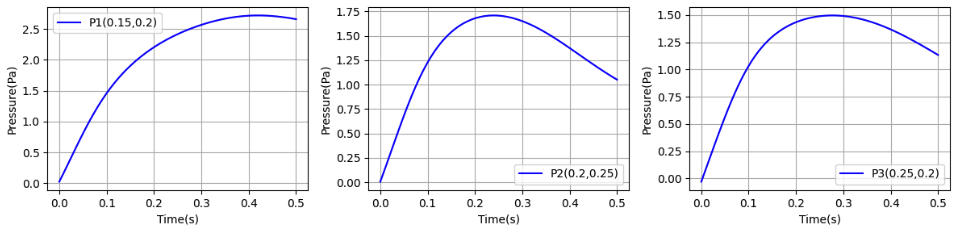
特定地点の圧力推移
速度場と圧力場
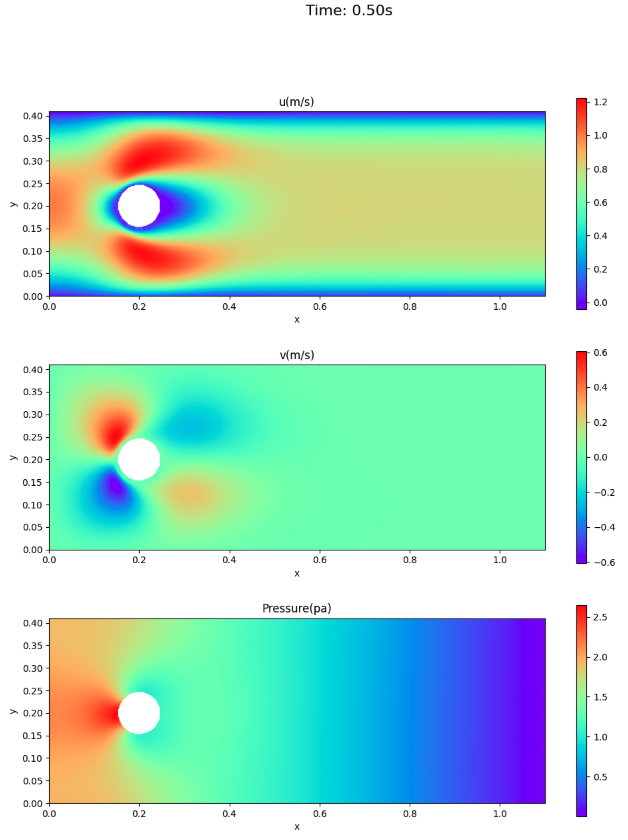
まとめ
ST型、VP型の両者を比較し、定性的には次のようなことが言える。
- ST型の方が、損失の収束が早い傾向にある。
- 3点の圧力については、ST型、VP型ともに情報源1.のカーブを異なる。圧力は、0.5秒時点でゼロ付近に戻っていない。最大値については、VP型の方が情報源1.の値に近い。
- 速度場については、VP型の方が、情報源1.に近い。
- 0.5秒後(1周期終了)時点でも円柱の前面に圧力が残っている。
学習率、エポック(ループ回数)を変更して、変化を見てみたい。
また、可視化結果を比較する際には、表示の尺度を揃えていないと目視での比較が困難であることが分かったので、そこも工夫の余地がある。